Hans Walser, [20160830]

KO-Mauern

Anregung: Th. W., Z.

1 Beispiel

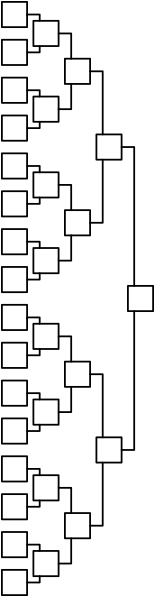
Die Abbildung 1 zeigt ein Beispiel einer KO-Mauer.

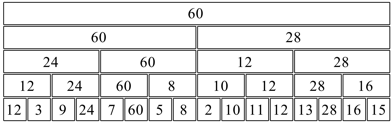
Abb. 1: KO-Mauer

2 Start

Das geht so: Wir beginnen mit der Mauergeometrie der Abbildung 2. Je zwei benachbarte Felder sind von einem Feld überdeckt.

Die Abbildung 2 findet sich im Anhang in größerem Format.

Abb. 2: Mauergeometrie

Dann füllen wir in der untersten Lage beliebige Zahlen ein. Die Zahlen sollen zufällig verteilt sein. Die Abbildung 3 zeigt ein Beispiel.

Die Zahlen dürfen auch negativ (zum Beispiel –7), gebrochen (zum Beispiel ¾) oder irrational (zum Beispiel π) sein.

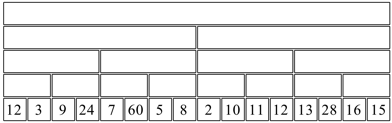
Abb. 3: Unterste Lage

3 Spielregel

In das Feld oberhalb zweier Felder wird die größere der beiden darunterliegenden Zahlen geschrieben. Bei zwei gleichen Zahlen wird diese ins obere Feld übernommen.

In diesem Spiel wird also nicht gerechnet, sondern lediglich verglichen.

Die kleinere Zahl fällt aus dem Spiel. Das ist wie bei einem KO-Turnier, daher der Name KO-Mauer. Wir werden im Folgenden auch die dem Sport entlehnten Begriffe erste Runde, zweite Runde, ... , Finale verwenden.

Spielvarianten:

· Selbstverständlich könnte auch mit der kleineren der beiden Zahlen gearbeitet werden.

· Statt Zahlen füllen wir Buchstaben ein und übernehmen jeweils denjenigen der beiden Buchstaben, welcher in alphabetischer Reihenfolge zuerst (oder zuletzt) kommt.

· Wir setzen Personennamen ein und übernehmen jeweils den schöneren Namen.

4 Einige Fragen

Welche Zahl steht am Schluss zuoberst (Sieger)?

Welche Zahlen kommen ins Finale?

Wenn wir die Zahlen in der untersten Lage umstellen dürfen: Welches ist die kleinstmögliche Zahl, die noch ins Finale kommen kann?

Wie viele Runden braucht es, bis der Sieger feststeht?

Welches ist die kleinste KO-Mauer?

Welches ist die mit der Abbildung 2 verglichen nächstgrößere KO-Mauer?

5 Sonderfälle

5.1 Eins, zwei, ...

Wir füllen die Zahlen 1, ... , 16 in ihrer natürlichen Reihenfolge in die unterste Lage (Abb. 4). Wie sieht der Spielverlauf aus?

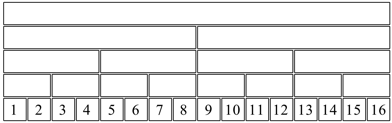
Abb. 4: 1, 2, ... , 16

In der ersten Runde fallen alle ungeraden Zahlen heraus, insbesondere auch die zweitgrößte Zahl 15. Im Spiel bleiben die geraden Zahlen.

In der zweiten Runde fallen die Zahlen 2, 6, 10, 14 heraus. Sie gehören zur arithmetischen Folge 2, 6, 10, 14, 18, ... .

Diese Zahlen kann man verschieden beschreiben. Euler nannte sie les nombres impairement pairs. Dies kann man mit die ungeraden geraden Zahlen übersetzen. Die Zahlen enthalten genau einen Primfaktor 2, also das Minimum, das noch zu einer geraden Zahl führt. Bei Division durch 2 erhalten wir eine ungerade Zahl. Innerhalb der Folge 2, 4, 6, 8, 10, ... der geraden Zahlen sind sie in den Positionen 1, 3, 5, ... , also in den ungeraden Positionen.

Im Spiel bleiben die Viererzahlen.

In der dritten Runde fallen diejenigen Viererzahlen heraus, die genau zwei Primfaktoren 2 haben.

Im Spiel bleiben die Achterzahlen. Und so weiter (Abb. 5).

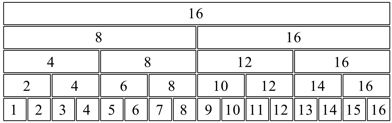
Abb. 5: 1, 2, ... , 16

5.2 Permutationen

Die Zahlen von 1 bis 16 können wir auf 16! = 20922789888000 verschiedene Arten in eine Reihenfolge bringen (permutieren) und entsprechend in der untersten Lage einsetzen. Das gibt jedes Mal eine andere KO-Mauer, aber immer ist 16 zuoberst.

Wie viele verschiedene solche KO-Mauern gibt es für jeden Erdenbewohner?

Die Abbildung 6 zeigt ein Beispiel.

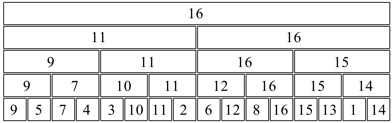
Abb. 6: Eine Permutation

Welche Permutation der Zahlen 1 bis 16 passt in die unterste Lage des Beispiels der Abbildung 7?

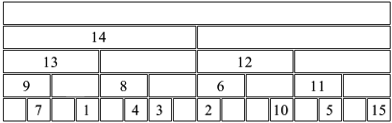
Abb. 7: Unterste Lage?

Für die Zahlen 1, 2, 3, 4 gibt es nur 4! = 24 Permutationen (Tab. 1).

Nummer	Permutation	Nummer	Permutation
1	[1, 2, 3, 4]	13	[3, 1, 2, 4]
2	[1, 2, 4, 3]	14	[3, 1, 4, 2]
3	[1, 3, 2, 4]	15	[3, 2, 1, 4]
4	[1, 3, 4, 2]	16	[3, 2, 4, 1]
5	[1, 4, 2, 3]	17	[3, 4, 1, 2]
6	[1, 4, 3, 2]	18	[3, 4, 2, 1]
7	[2, 1, 3, 4]	19	[4, 1, 2, 3]
8	[2, 1, 4, 3]	20	[4, 1, 3, 2]
9	[2, 3, 1, 4]	21	[4, 2, 1, 3]
10	[2, 3, 4, 1]	22	[4, 2, 3, 1]
11	[2, 4, 1, 3]	23	[4, 3, 1, 2]
12	[2, 4, 3, 1]	24	[4, 3, 2, 1]

Tab. 1: Permutationen der Zahlen 1, 2, 3, 4

Die Abbildung 8 zeigt die KO-Mauer für die Permutation 14.

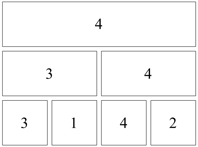
Abb. 8: Permutation 14

Wie lassen sich die Permutationen mit einem Computerprogramm auflisten?

5.3 Verdoppelungsfolge

Wir starten mit der Folge 2, 4, 8, 16, ... . Da die Zahlen sehr groß werden (2⁸ =256, aber 2¹⁶ = 65536) arbeiten wir mit einer kleineren KO-Mauer (Abb. 9).

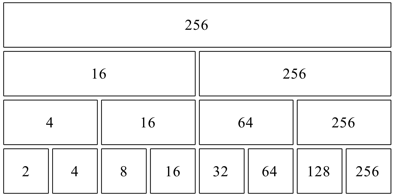
Abb. 9: Verdoppelungsfolge

Was erhalten wir, wenn wir mit der 1 beginnen: 1, 2, 4, 8, ... ?

6 Geometrie der KO-Mauer

6.1 Verschiedene Größen

Wir haben schon gesehen dass wir in der untersten Lage 2 oder 4 oder 8 oder 16, allgemein 2ⁿ Felder brauchen. Wir haben dann n + 1 Lagen übereinander. Das Spiel braucht n Runden.

6.2 Verschiedene Formen

Es gibt verschiedene geometrische Formen zur Gestaltung einer KO-Mauer. Im Beispiel der Abbildung 2 haben wir in der untersten Lage Quadrate. Alle Felder sind gleich hoch, aber die Längen verdoppeln sich von Lage zu Lage.

In der Abbildung 10 sind alle Felder Quadrate.

Abb. 10: Quadratische Felder

In der Abbildung 11 sind alle Felder halb so hoch wie breit.

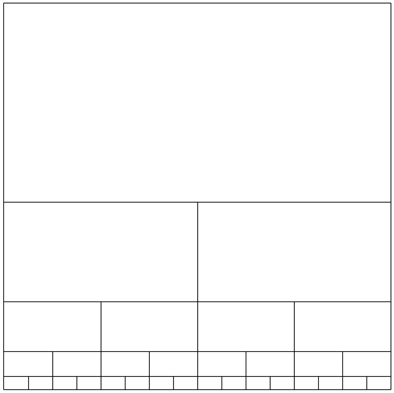
Abb. 11: Felder halb so hoch wie breit

In der Abbildung 12 sind die quadratischen Felder übereck positioniert. Alle Felder haben Bodenkontakt.

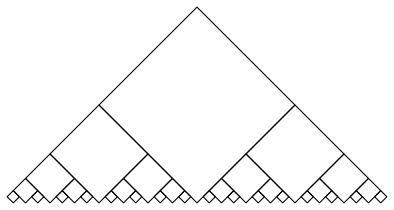
Abb. 12: Übereck-Quadrate

Die Abbildung 13 zeigt eine schematische Darstellung. Die Abbildung 13 findet sich im Anhang in größerem Format.

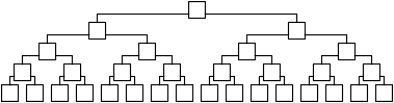
Abb. 13: Schematische Darstellung

6.3 Verschiedene Farben

Statt Zahlen oder Buchstaben können wir auch mit Farben arbeiten. Dazu müssen wir eine Rangreihenfolge unter den beteiligten Farben festlegen.

Die Abbildung 14 zeigt die 4! = 24 möglichen KO-Mauern mit vier Farben in der untersten Lage. Die gewählte Rangreihenfolge ist aus der Abbildung 14 ersichtlich. Die Permutationen sind spaltenweise angeordnet. Die erste Spalte enthält die Permutationen 1 bis 6 gemäß Tabelle 1.

Abb. 14: Vier Farben

7 Anhang