Hans Walser, [20080922a]
Kaleidoskop
Anregung: J. S.
In einen
Zylinder mit gegebenem Innenradius r
sollen 
Spiegel der Dicke
d zu einem Kaleidoskop eingepasst
werden (Figur fźr das klassische Kaleidoskop mit 
). Gesucht ist die Spiegelbreite b.
Kaleidoskop
Bearbeitung
Wir
arbeiten mit dem in der folgenden Figur eingezeichneten Dreieck. Dieses hat den
stumpfen Winkel 
.
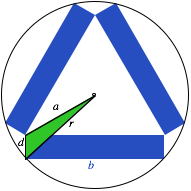
Arbeitsfigur
ZunŠchst
ist 
. Der Kosinussatz im Dreieck liefert:
Daraus ergibt sich die quadratische Gleichung fźr a:
Diese hat die positive Lšsung:
Wegen 
erhalten wir fźr
die gesuchte Spiegelbreite:
Fźr das klassische Kaleidoskop mit 3 Spiegeln erhalten wir daraus:
Bemerkung: Bei dieser Lšsung treffen zwei benachbarte Spiegel entlang einer gemeinsamen Kante aufeinander. Das ist statisch sehr ungźnstig und dźrfte in der Praxis kaum funktionieren.