Hans Walser, [20130506]
Kardioide als Spiegelbild der Parabel bei Kreisspiegelung
1 Die Parabel
Wir beschreiben die Parabel durch:
![]()
Es handelt sich um eine ãliegendeÒ Parabel (Abb. 1). Der Ursprung ist der Brennpunkt.

Abb. 1: Liegende Parabel
2 Spiegelung am Einheitskreis
Bei der Spiegelung am
blauen Einheitskreis wird ein Punkt P(x,y) auf den Punkt ![]() abgebildet. Die
Abbildungsgleichungen sind:
abgebildet. Die
Abbildungsgleichungen sind:
![]()
Die Punkte au§erhalb des blauen Einheitskreises werden ins Innere abgebildet und umgekehrt, der Ursprung wird in den unendlich fernen Punkt abgebildet. Der Einheitskreis bleibt punktweise fix.
Die Abbildung 2 zeigt die grne Parabel und ihr rotes Spiegelbild bei der Spiegelung am blauen Einheitskreis.
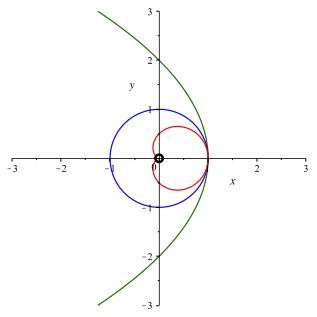
Abb. 2: Spiegelbild
Wir vermuten, dass das rote Spiegelbild der grnen Parabel die Kardioide ist.
3 Beweis
Wir beweisen umgekehrt, dass das Spiegelbild der Kardioide die Parabel ist. Fr die Kardioide haben wir die Parameterdarstellung:
![]()
Die Abbildungsgleichungen der Rckspiegelung sind:
![]()
Wegen
![]()
erhalten wir:
![]()
Wir haben die
Parabelgleichung ![]() zu verifizieren,
also:
zu verifizieren,
also:
![]()
Dies kann leicht nachgerechnet werden.
4 Enveloppen
Die Parabel kann als Enveloppe ihrer Tangenten dargestellt werden (Abb. 3).
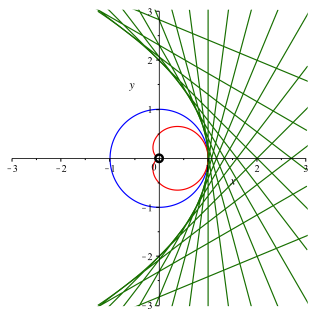
Abb. 3: Parabel als Enveloppe
Der Fu§punkt des Lotes
vom Ursprung auf eine solche Tangente liegt auf der schwarzen Geraden ![]() (Abb. 4). Diese
schwarze Gerade ist die Scheiteltangente der Parabel.
(Abb. 4). Diese
schwarze Gerade ist die Scheiteltangente der Parabel.
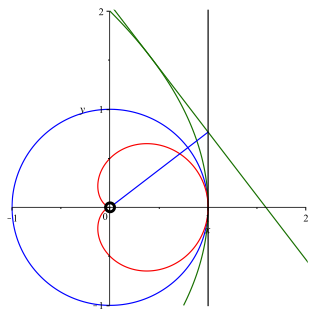
Abb. 4: Lotfu§punkt
Nun spiegeln wir die grne Tangente und die schwarze Scheiteltangente am blauen Einheitskreis (Abb. 5). Beide werden zu Kreisen durch den Ursprung. Der rote Bildkreis der grnen Tangente ist Thaleskreis ber der Strecke, welche durch den schwarzen Kreis aus dem Lot auf die grne Tangente herausgeschnitten wird.
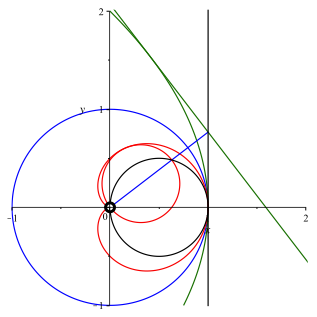
Abb. 5: Spiegeln der Tangente
Die Abbildung 6 zeigt zustzlich den Berhrungspunkt der grnen Tangente mit der Parabel einerseits und den Berhrungspunkt des roten Bildkreises, des Thaleskreises also, mit der Kardioide.
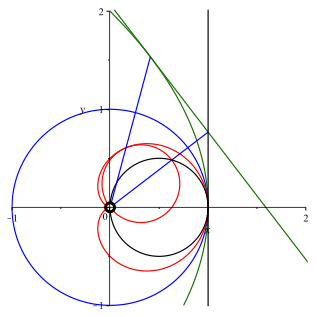
Abb. 6: Berhrungspunkte
In der Abbildung 7 schlie§lich ist die Kardioide als Enveloppe der Thaleskreise dargestellt.
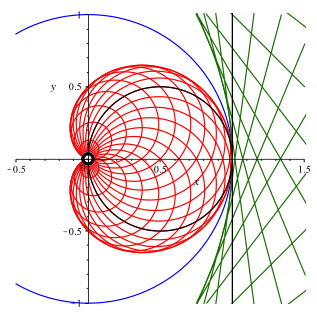
Abb. 7: Kardioide als Enveloppe
Der sthetik halber das Ganze gekippt (Abb. 8).
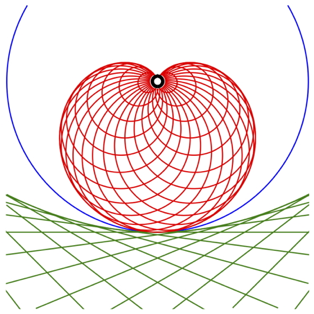
Abb. 8: Parabel und Kardioide