1 Worum geht es?

Die Kardioide ist Enveloppe von Möndchen des Hippokrates. Beweis.

2 Kardioide als Lotfußpunktkurve

In der folgenden Darstellung werden Punkte und ihre Ortsvektoren identifiziert.

Auf dem Einheitskreis wählen wir einen Punkt (Abb. 1) und zeichnen die Kreistangente durch diesen Punkt.

Abb. 1: Tangente

Vom Punkt aus zeichnen wir das Lot auf die Tangente (Abb. 2). Der Schnittpunkt mit der Tangente, also der Lotfußpunkt, sei P. Wegen ist:

(1)

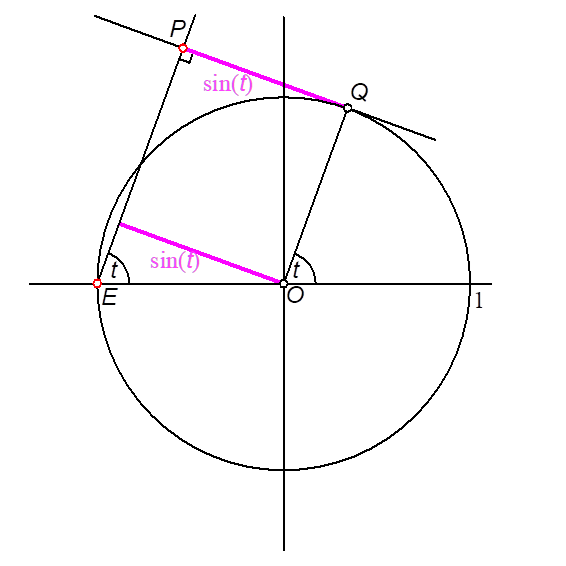
Abb. 2: Lotfußpunkt

Variation von führt zur Kardioide (Abb. 3).

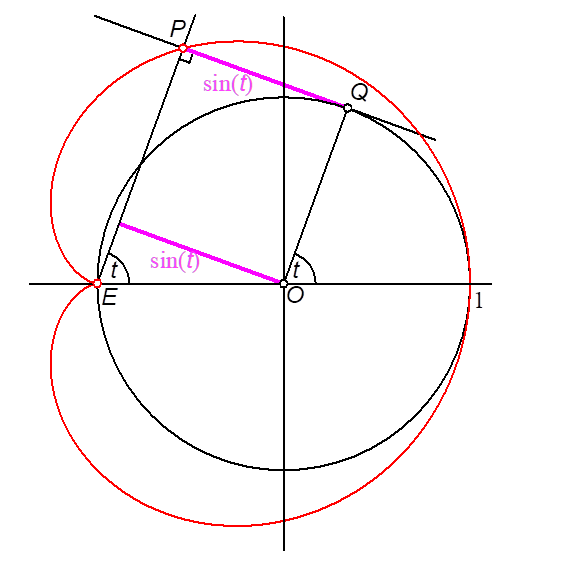
Abb. 3: Kardioide

Die Kardioide hat in P den Tangentialvektor:

(2)

3 Thaleskreis

Der Thaleskreis über der Strecke EQ verläuft durch den Punkt P (Abb. 4). Der Thaleskreis hat den Mittelpunkt N:

(3)

Der Vektor

(4)

ist der Normalvektor zum Thaleskreis.

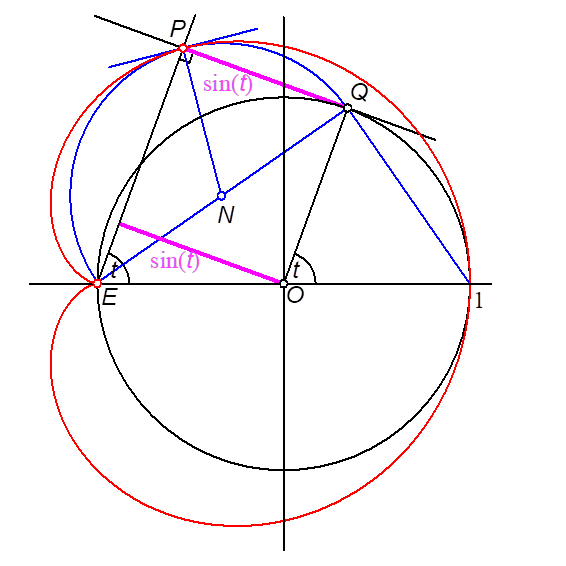
Abb. 4: Thaleskreis

4 Skalarprodukt

Das Skalarprodukt der Vektoren (2) (Tangentialvektor an die Kardioide in P) und (4) (Normalvektor des Thaleskreises in P) ist null. Daher berührt der Thaleskreis in P die Kardioide.

Der Thaleskreis ist Außenkreis eines Möndchens von Hippokrates (Abb. 5).

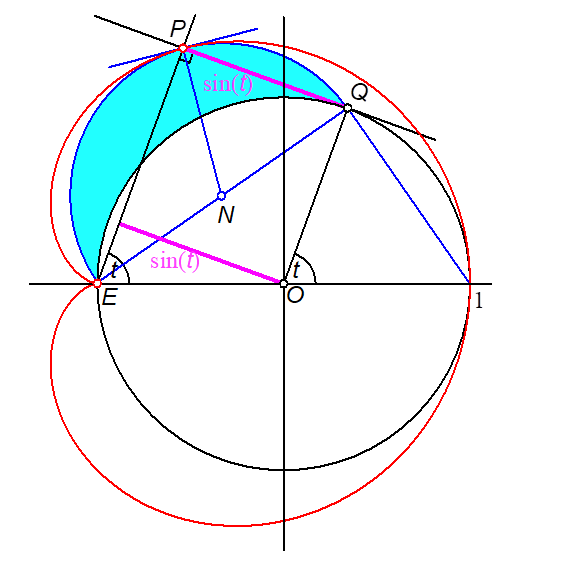
Abb. 5: Möndchen des Hippokrates

Die Animation 1 visualisiert den Sachverhalt.

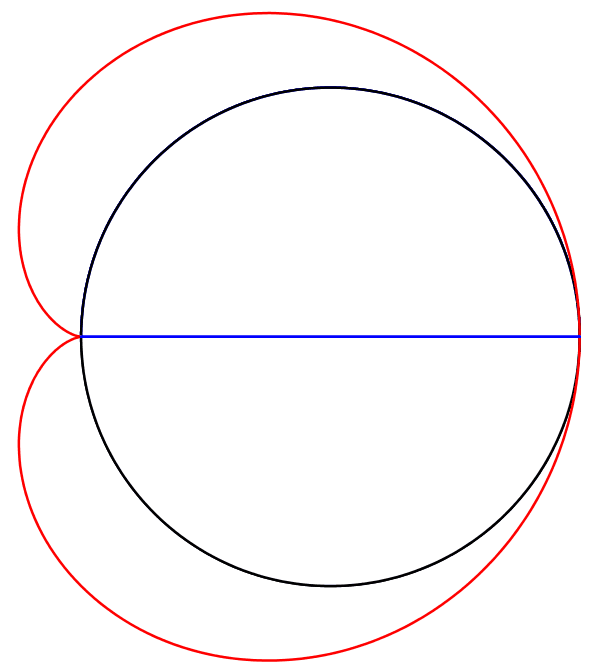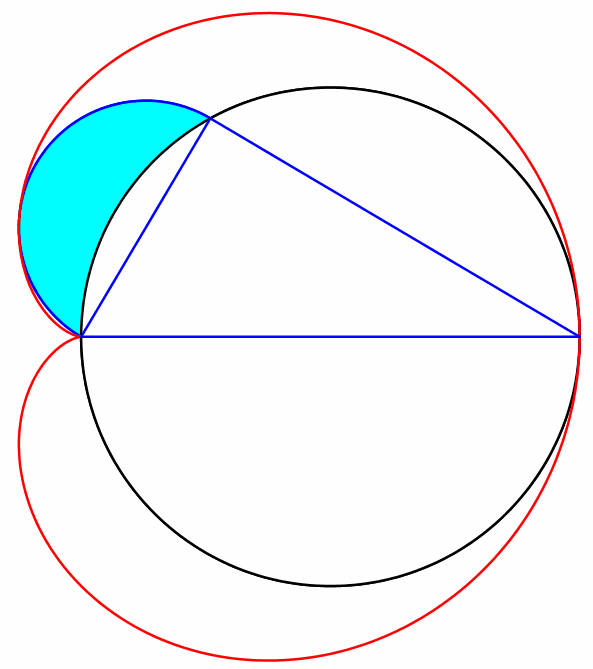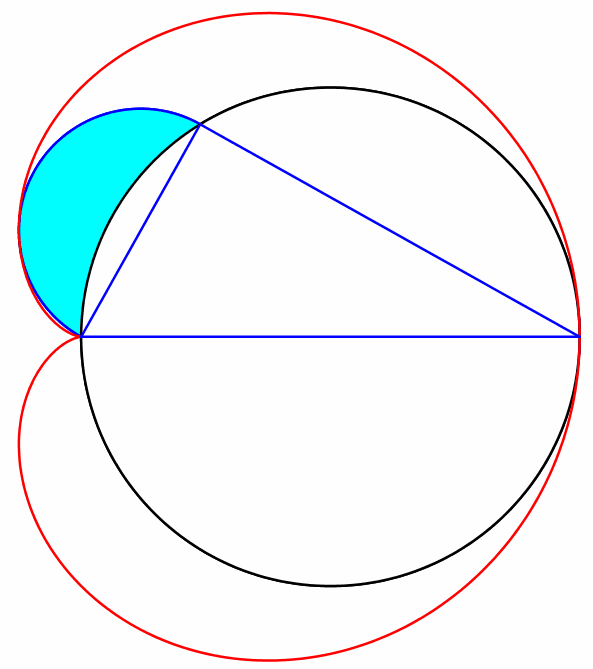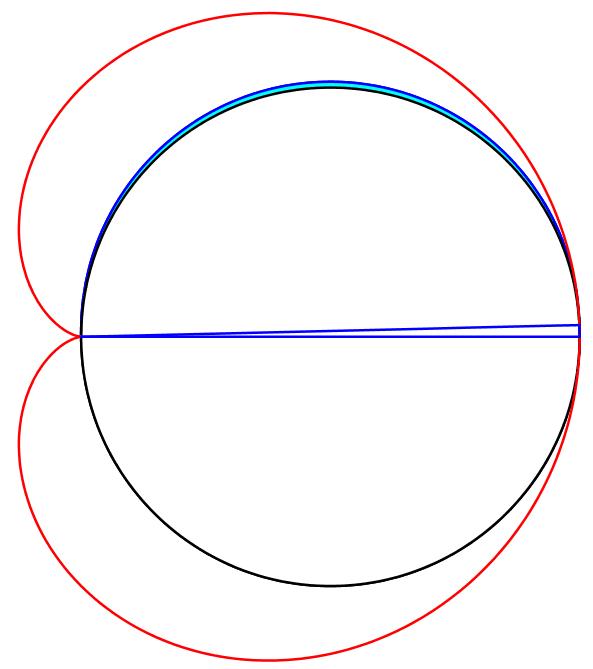
Animation 1

Weblinks

Hans Walser: Kardioide und regelmäßige Vielecke

http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide3/Kardioide3.htm

Hans Walser: Al-Sijizi

http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/index.html

Hans Walser: Die Herzkurve und die Möndchen des Hippokrates

www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm

Hans Walser: Herzkurve als Enveloppe

http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm

Hans Walser: Kardioide als Spiegelbild der Parabel bei Kreisspiegelung

http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm

Hans Walser: Kardioide und Goldener Schnitt

http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide/Kardioide.htm

Hans Walser: Umkreis bei regelmäßigen Vielecken

http://www.walser-h-m.ch/hans/Miniaturen/U/Umkreis/index.html