Hans Walser, [20210101]

Kardioide

1     Worum geht es?

Kardioide im Umfeld von rechtwinkligen Dreiecken, Thaleskreis und logarithmischen Spiralen.

2     Thaleskreis

Zu einem rechtwinkligen Dreieck zeichnen wir den Thaleskreis (Abb. 1).

Abb. 1: Rechtwinkliges Dreieck und Thaleskreis

Wir kšnnen mit dem Eckpunkt beim rechten Winkel auf dem Thaleskreis spazieren gehen (Abb. 2).

 

020.gif

Abb. 2: Bewegung im Thaleskreis

3     Ansetzen eines Šhnlichen Dreiecks

Wir setzen der einen Kathete des Dreiecks ein dazu Šhnliches Dreieck an (Abb. 3). Die Hypotenuse des blauen Dreiecks ist gleich der Ansetzkathete des roten.

Abb. 3: Ansetzen eines Šhnlichen Dreiecks

4     Bahnkurve

Wir bewegen nun beim roten Dreieck den Eckpunkt mit dem rechten Winkel auf dem Thaleskreis gemŠ§ Abbildungen 1 und 2. Welche Kurve beschreibt dabei der Eckpunkt mit dem rechten Winkel des blauen Dreiecks (Abb. 4)?

 

040.gif

Abb. 4: Bahnkurven

Die Bahnkurve ist die gute alte Kardioide.

5     Beweis

Die blaue Bahnkurve ist die Lotfu§punktkurve (Pedalkurve) des roten Thaleskreises (Abb. 5) und damit eine Kardioide. Die Lote gehen vom linken Punkt auf dem Thaleskreis aus und werden mit den Thaleskreistangenten geschnitten.

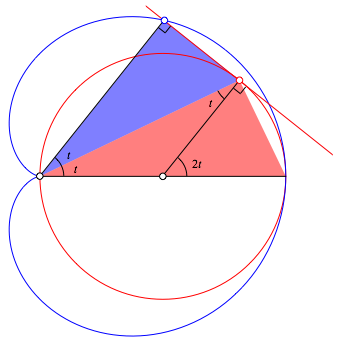
Abb. 5: Lotfu§punktkurve

6     Parameterdarstellung

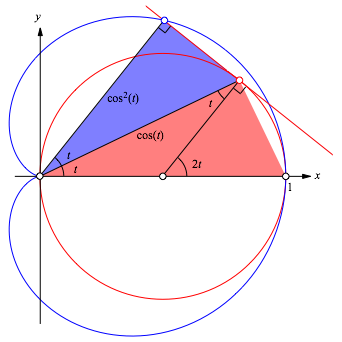
Abb. 6: Im Koordinatensystem

Im Koordinatensystem der Abbildung 6 erhalten wir fŸr die Kardioide  die Parameterdarstellung:

 

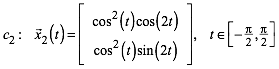                                             (1)

 

 

 

 

 

Ebenso erhalten wir fŸr den roten Thaleskreis  die Parameterdarstellung:

 

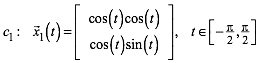                                                   (2)

 

 

 

 

 

7     Wie geht es weiter?

FŸr n = 3 ergibt sich die Kinematik der Abbildung 7.

 

070.gif

Abb. 7: Drei Dreiecke

Die Šu§erste Bahnkurve  hat die Parameterdarstellung:

 

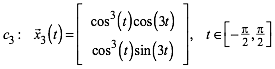                                              (3)

 

 

 

 

 

Sie ist ebenfalls eine Lotfu§punktkurve (Abb. 8), und zwar die Lotfu§punktkurve der Kardioide . Die Lote gehen wiederum vom linken Punkt auf dem Thaleskreis aus, werden jetzt aber mit den Tangenten an die Kardioide geschnitten.

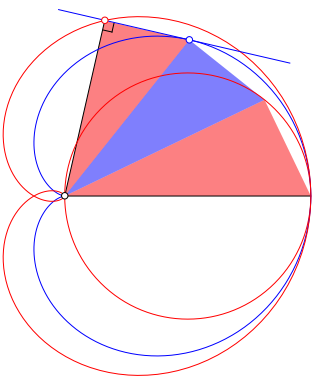
Abb. 8: Lotfu§punktkurve

Wir beweisen das gleich allgemein im ŸbernŠchsten Abschnitt.

8     Allgemein

FŸr die Kurve  haben wir die Parameterdarstellung:

 

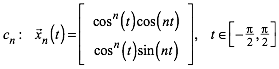                                             (4)

 

 

 

 

 

Die Abbildung 9 zeigt die Kurven fŸr n = 1 bis 14.

Abb. 9: Die ersten 14 Kurven

In der Abbildungen 10 und 11 ist die zugehšrige Schnecke mit den rechtwinkligen Dreiecken eingezeichnet. Die Eckpunkte liegen auf einer logarithmischen Spirale.

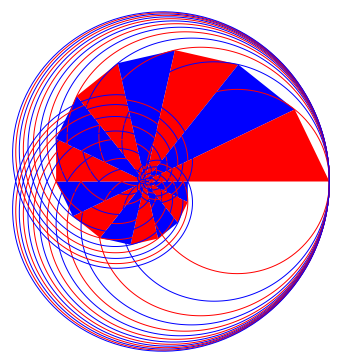
Abb. 10: Schnecke

 

110.gif

Abb. 11: Dynamische Schnecke

Die Abbildung 12 zeigt die Kurven fŸr n = 1 bis 28, der Gravitation zuliebe in einer bilateralen Symmetrie.

Der Umriss der Kurvenschar nŠhert sich einem Kreis, der doppelt so gro§ ist wie der ursprŸngliche Thaleskreis.

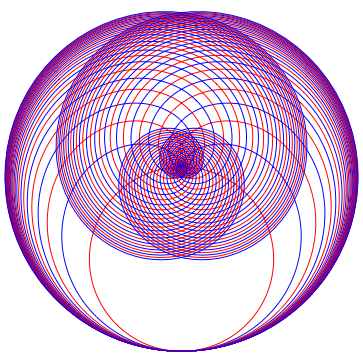
Abb. 12: Die ersten 28 Kurven

9     Rekursion

Es gilt:  ist Fu§punktkurve von , also die Menge der Schnittpunkte der Tangenten an  mit den vom Ursprung ausgehenden Loten.

Wir haben zu zeigen: Der Tangentialvektor  ist orthogonal zu .

Aus (4) erhalten wir:

 

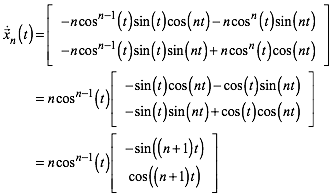                           (5)

 

 

 

 

 

 

 

 

 

Weiter ergibt sich aus (4):

 

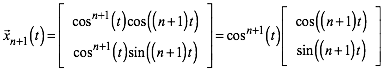         (6)

 

 

 

 

 

Die beiden Vektoren (5) und (6) haben das Skalarprodukt null und sind orthogonal. Dies war zu zeigen.

10  BogenlŠnge und FlŠcheninhalt

Aus (5) ergibt sich zunŠchst

 

 

                                                                                                 (7)

 

 

 

 

und daraus fŸr die BogenlŠnge  der Kurve :

 

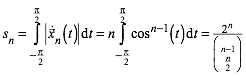                                                       (8)

 

 

 

 

 

FŸr den FlŠcheninhalt  ergibt sich aus (4) und (5) nach dem Integralsatz von Stokes mit einiger Rechnung:

 

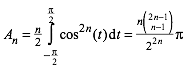                                                                           (9)

 

 

 

 

Die Tabelle 1 gibt die ersten Werte. Bei der BogenlŠnge kommt alternierend die Kreiszahl  vor.

 

n

BogenlŠnge

numerisch

FlŠcheninhalt

numerisch

1

Pi

3.141592654

1/4*Pi

0.7853981635

2

4

4

3/8*Pi

1.178097245

3

3/2*Pi

4.712388981

15/32*Pi

1.472621557

4

16/3

5.333333333

35/64*Pi

1.718058483

5

15/8*Pi

5.890486226

315/512*Pi

1.932815793

6

32/5

6.4

693/1024*Pi

2.126097372

7

35/16*Pi

6.872233931

3003/4096*Pi

2.303272153

8

256/35

7.314285714

6435/8192*Pi

2.467791593

9

315/128*Pi

7.731263172

109395/131072*Pi

2.622028567

10

512/63

8.126984127

230945/262144*Pi

2.767696821

Tab. 1: BogenlŠngen und FlŠcheninhalt

 

 

 

Websites

Hans Walser: Al-Sijizi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/index.html

Hans Walser: Die Herzkurve und die Mšndchen des Hippokrates
www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm

Hans Walser: Herzkurve als Enveloppe
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm

Hans Walser: Kardioide als Enveloppe
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide4/Kardioide4.htm

Hans Walser: Kardioide als Spiegelbild der Parabel bei Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm

Hans Walser: Kardioide und Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide/Kardioide.htm

Hans Walser: Kardioide und regelmŠ§ige Vielecke
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide3/Kardioide3.htm

Hans Walser: Krumme Wellenlinie
http://www.walser-h-m.ch/hans/Miniaturen/K/Krumme_Wellenlinie/Krumme_Wellenlinie.htm

Hans Walser: Umkreis bei regelmŠ§igen Vielecken
http://www.walser-h-m.ch/hans/Miniaturen/U/Umkreis/index.html