Hans Walser, [20210102]

Kardioide

1     Worum geht es?

Spielereien um die Kurvenschar:

 

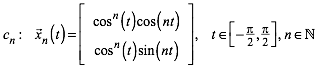                               (1)

 

 

 

 

 

Viele Bilder

2     Einstieg

FŸr n = 1 ergibt sich der Kreis (rot in Abb. 1), fŸr n = 2 die Kardioide (blau in Abb. 1).

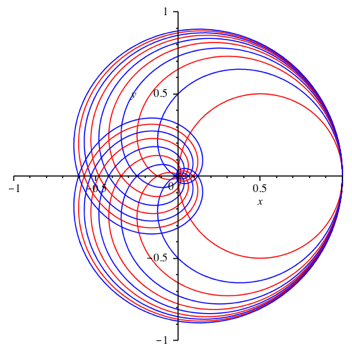
Abb. 1: Kurvenschar

FŸr grš§ere Werte von n haben wir verallgemeinerte Kardioiden.

3     Ganzzahlige Indizes

Wir ersetzen  durch . Wegen  mŸssen wir den Definitionsbereich etwas einschrŠnken, um eine Division durch null zu vermeiden:

 

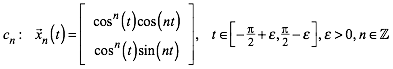      (2)

 

 

 

 

 

Die Abbildung 2 zeigt die Kurven fŸr .

FŸr n = 0 ergibt sich der Einheitspunkt auf der positiven x-Achse.

FŸr n = –1 erhalten wir die senkrechte Gerade x = 0.

FŸr n = –2 ergibt sich die liegende Parabel .

 

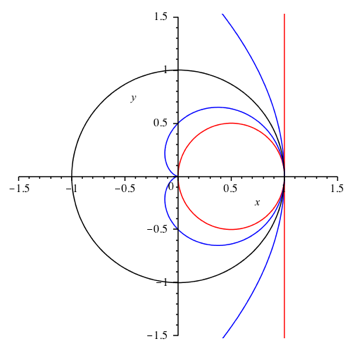
Abb. 2: Kreisspiegelung

Es sieht nun so aus, dass  und  (sie haben jeweils dieselbe Farbe) durch eine Kreisspiegelung am Einheitskreis auseinander hervor gehen. Dies ist global gesehen richtig, punktweise gesehen kommt aber noch eine Spiegelung an der x-Achse dazu. Dies sehen wir, wenn wir den Definitionsbereich fŸr t asymmetrisch wŠhlen. Die Abbildung 3 zeigt die Kurvenschar:

 

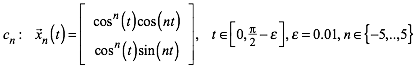  (3)

 

 

 

 

 

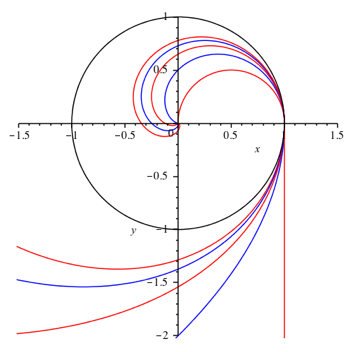
Abb. 3: Asymmetrie

Die Kurven mit entgegengesetzt gleichem Index gehen zwar glatt (ohne RichtungsŠnderung) ineinander Ÿber, haben aber an der †bergangsstelle einen KrŸmmungssprung.

Die Abbildung 4 zeigt die Variante:

 

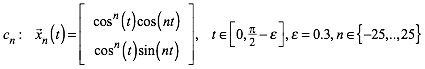          (4)

 

 

 

 

 

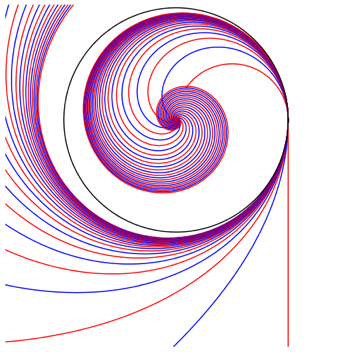
Abb. 4: Variante

4     Rationale Indizes

Die Sache funktioniert auch fŸr rationale Indizes. Die Abbildung 5 zeigt die Situation fŸr:

 

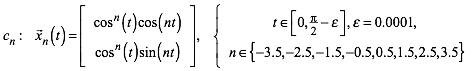 (5)

 

 

 

 

 

Man beachte den Farbwechsel bei der Kreisspiegelung.

 

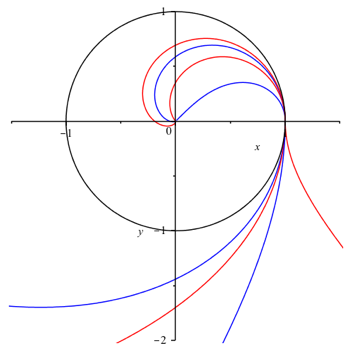
Abb. 5: Halbzahlige Indizes

5     Vertauschung

In (1) vertauschen wir die Rollen von n und t. Das sieht exemplarisch so aus:

 

 

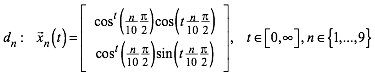             (6)

 

 

 

 

 

Die Kurvenschar besteht aus logarithmischen Spiralen (Abb. 6).

 

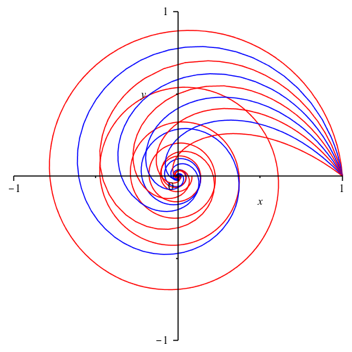
Abb. 6: Logarithmische Spiralen

6     FlŠche im Raum

Aus (1) basteln wir eine Parameterdarstellung einer FlŠche im Raum:

 

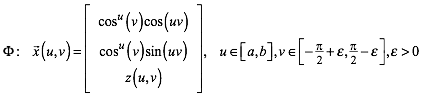          (7)

 

 

 

 

 

Die z-Koordinate ist noch frei wŠhlbar.

FŸr z = 0 erhalten wir eine ebene Figur (Abb. 7 fŸr a = 0 und b = 2).

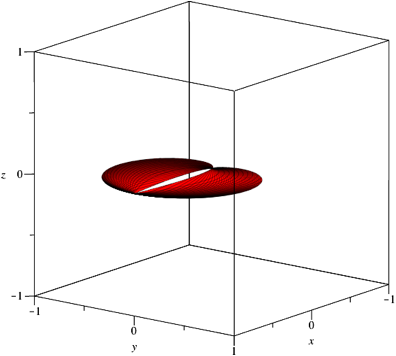
Abb. 7: Ebene Figur

Die Abbildung 8 zeigt die Sicht von oben (Grundriss). Der Umriss ist die Kardioide. Die u-Linien sind logarithmische Spiralen, die v-Linien verallgemeinerte Kardioiden.

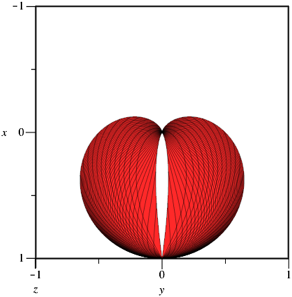
Abb. 8: Kardioide

FŸr  ergibt sich die FlŠche der Abbildung 9. Die oberste Niveaulinie ist die Kardioide.

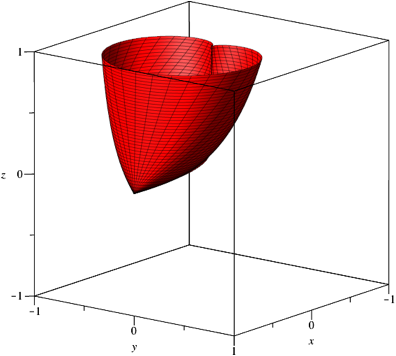
Abb. 9: Niveaulinien verallgemeinerte Kardioiden

Mit  erhalten wir die FlŠche der Abbildung 10. Die Niveaulinien sind logarithmische Spiralen.

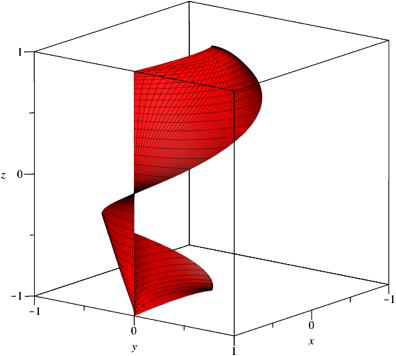
Abb. 10: Niveaulinien logarithmische Spiralen

 

Websites

Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide5/Kardioide5.htm

Hans Walser: Kardioide als Spiegelbild der Parabel bei Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm