Hans Walser, [20210117]

Kardioide und invariante Flächen

Anregung: Stephan Berendonk, Köln

1 Worum geht es?

Ein klassisches Beispiel für eine invariante Flächensumme sind die beiden Kathetenquadrate beim rechtwinkligen Dreieck, wenn die Ecke mit dem rechten Winkel auf dem Thaleskreis bewegt wird.

Bei der Kardioide gibt es einen ähnlichen Sachverhalt.

2 Kardioide und Fächer

An der einwärts gerichteten Spitze einer Kardioide (Abb. 1a) setzen wir einen regelmäßigen n-teiligen Fächer an (Abb. 1b für n = 5). Die Fächergeraden schneiden wir mit der Kardioide.

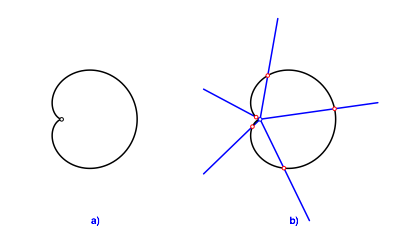
Abb. 1: Kardioide und Fächer

Ausblick: Was ist los mit den Kardioidentangenten in den Schnittpunkten?

Die Schnittpunkte definieren ein n-Eck (Abb. 2a). Den Seiten des n-Ecks setzen wir Quadrate an (Abb. 2b).

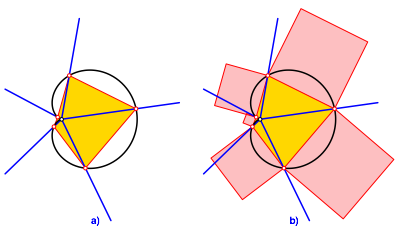
Abb. 2: Vieleck und Quadrate

Nun drehen wir den Fächer um sein Zentrum (Abb. 3 und 4). Dann gilt folgendes:

Der Flächeninhalt des n-Ecks bleibt invariant.

Die Flächensumme der n Quadrate bleibt invariant.

Abb. 3: Drehen des Fächers

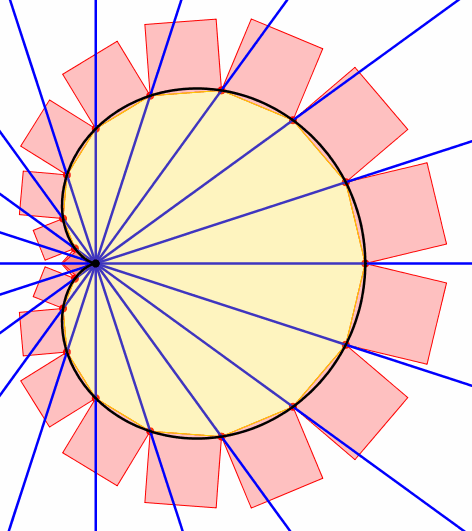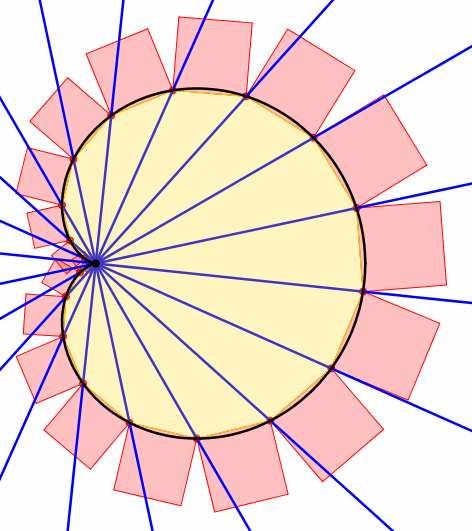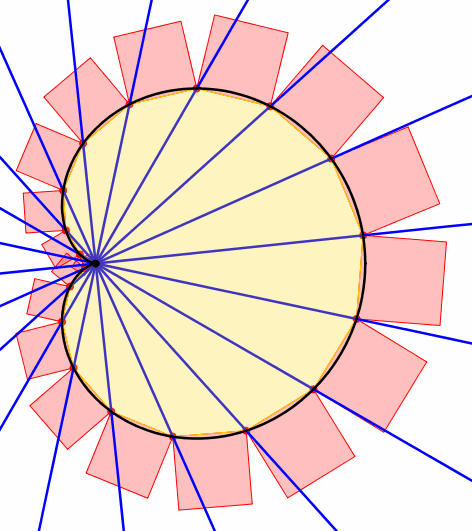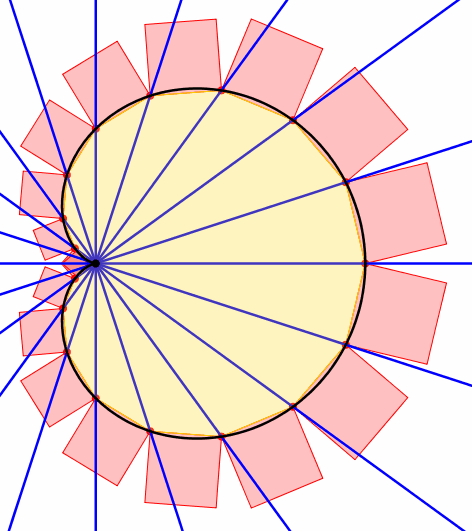
Abb. 4: 20-teiliger Fächer

3 Beweise

3.1 Formeln auf Vorrat

Ich weiß, ich weiß, das Anlegen eines Formelvorrates ist didaktisch verpönt. Es widerspricht den hehren Prinzipien von entdeckendem Lernen und projektorientiertem Arbeiten. Aber der Kuchen kann erst gegessen werden, wenn er gebacken ist.

3.1.1 Summe und Differenz von Winkeln

Aus den Additionstheoremen folgt:

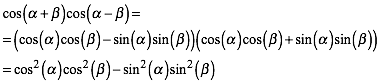(1)

Analog:

(2)

3.1.2 Zyklische Summen

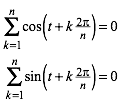(3)

Beweis: Die Vektoren

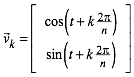(4)

lassen sich zu einem geschlossenen regelmäßigen n-Eck zusammenfügen (Abb. 5 für n = 5). Dabei ist t der Verdrehungswinkel der Figur. Auf das Resultat in (3) hat er keinen Einfluss. Hier tritt zum ersten Mal das Phänomen der Invarianz auf.

Abb. 5: Umordnen der Vektoren

Etwas allgemeiner:

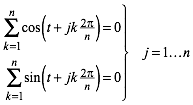(5)

Die Abbildung 6 deutet den Beweis für n = 5 und j = 2 an. Wie ist es, wenn j ein Teiler von n ist?

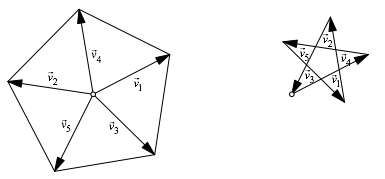
Abb. 6: Weihnachten kommt bestimmt

3.1.3 Zyklische Summen mit Quadraten

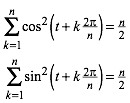(6)

Herleitung: Aus dem Additionstheorem für den Kosinus ergibt sich:

(7)

Daher ist:

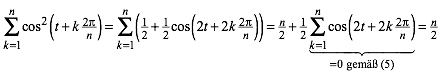(8)

Statt t fällt jetzt 2t heraus.

Damit ist die erste Zeile von (6) gezeigt. Da die Summe der beiden linken Seiten von (6) den Wert n ergibt, folgt die zweite Zeile von (6).

3.1.4 Zyklische Summe eines Produktes

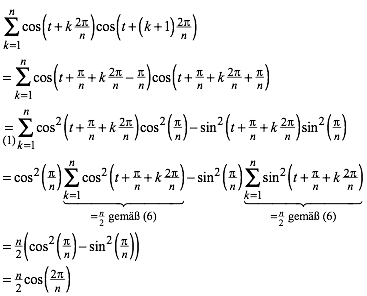(9)

Statt t fällt jetzt weg.

Und nun zur Sache.

3.2 Kardioidendarstellung

Für den Beweis arbeiten wir mit der Kardioidendarstellung in Polarkoordinaten:

(10)

Die Einwärtsspitze kommt in den Ursprung zu liegen (Abb. 7).

In der Abbildung 7 ist ein um t = 26° verdrehter Fächer mit n = 20 Strahlen eingezeichnet.

Abb. 7: Beweisfigur

3.3 Flächenberechnungen

3.3.1 Das Vieleck

Für das gelbe Dreieck erhalten wir den Flächeninhalt:

(11)

Somit ergibt sich für den Flächeninhalt A des gelben n-Ecks (Abb. 2a):

(12)

Der Drehparameter fällt weg. Damit ist die Invarianz bewiesen.

Die Tabelle gibt den invarianten Flächeninhalt des n-Eckes für n = 3 ... 12.

n	Flächeninhalt	numerisch
3	9/16*3^(1/2)	0.9742785795
4	2	2.
5	5/2*sin(2/5*Pi)+5/8*sin(1/5*Pi)	2.745007074
6	15/8*3^(1/2)	3.247595265
7	7/2*sin(2/7*Pi)+7/8*sin(3/7*Pi)	3.589472112
8	2*2^(1/2)+1	3.828427124
9	9/2*sin(2/9*Pi)+9/8*sin(4/9*Pi)	4.000452966
10	5*sin(1/5*Pi)+5/4*sin(2/5*Pi)	4.127746908
11	11/2*sin(2/11*Pi)+11/8*sin(4/11*Pi)	4.224268490
12	3+3/4*3^(1/2)	4.299038106

Tab. 1: Flächeninhalt

Für wird (CAS). Das ist der Flächeninhalt der Kardioide.

3.3.2 Die Quadrate

Für die Seitenlänge s_k und die Quadratfläche dazu (Abb. 7) finden wir mit dem Kosinussatz:

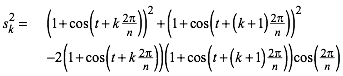(13)

Beim Aufsummieren erhalten wir unter Benützung der Formeln in Abschnitt 3.1:

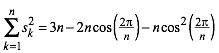(14)

Wiederum fällt der Drehparameter t weg. Damit ist die Invarianz der Quadratsumme nachgewiesen.

Die Tabelle 2 gibt die invariante Quadratsumme für n = 3 ... 12.

n	Quadratsumme	numerisch
3	45/4	11.25
4	12	12.
5	15-10*cos(2/5*Pi)-5*cos(2/5*Pi)^2	11.43237255
6	21/2	10.5
7	21-14*cos(2/7*Pi)-7*cos(2/7*Pi)^2	9.549966050
8	20-8*2^(1/2)	8.68629150
9	27-18*cos(2/9*Pi)-9*cos(2/9*Pi)^2	7.929783221
10	30-20*cos(1/5*Pi)-10*cos(1/5*Pi)^2	7.274575139
11	33-22*cos(2/11*Pi)-11*cos(2/11*Pi)^2	6.707639710
12	27-12*3^(1/2)	6.21539030

Tab. 2: Quadratsummen

Für wachsende n verschwindet die Quadratsumme.

Websites

Hans Walser: Al-Sijizi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/index.html

Hans Walser: Die Herzkurve und die Möndchen des Hippokrates
www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm

Hans Walser: Herzkurve als Enveloppe
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm

Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide5/Kardioide5.htm

Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide6/Kardioide6.htm

Hans Walser: Kardioide
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide8/Kardioide8.htm

Hans Walser: Kardioide als Enveloppe
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide4/Kardioide4.htm

Hans Walser: Kardioide als Spiegelbild der Parabel bei Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm

Hans Walser: Kardioide als Spiegelbild der Parabel bei Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide2/Kardioide2.htm

Hans Walser: Kardioide und Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide/Kardioide.htm

Hans Walser: Kardioide und regelmäßige Vielecke
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide3/Kardioide3.htm

Hans Walser: Kardioide und Thaleskreis
http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide7/Kardioide7.htm

Hans Walser: Umkreis bei regelmäßigen Vielecken
http://www.walser-h-m.ch/hans/Miniaturen/U/Umkreis/index.html