Hans Walser, [20190328]
Karospirale
Anregung: Hans-Peter Stricker, Berlin
1 Worum geht es?
Quadrate werden zu einer archimedischen Spirale aufgereiht.
2 Spirale und Punkte
Die Abbildung 1 zeigt eine archimedische Spirale.
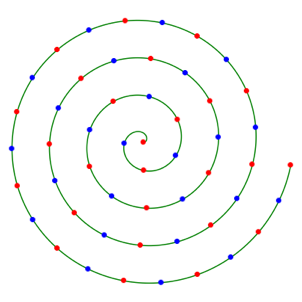
Abb. 1: Spirale und Punkte
Auf der Spirale sind in gleichen AbstŠnden Punkte gezeichnet. Dabei sind die gleichen AbstŠnde jeweils auf der Spirale gemessen. Es handelt sich also nicht um euklidische AbstŠnde.
3 Kreise und Zahlen
Wir zeichnen Kreise um die Punkte und versehen die Kreise mit den natźrlichen Zahlen, beginnend bei null (Abb. 2). Der Durchmesser der Kreise ist gleich dem Abstand der Punkte in der Abbildung 1. Da dieser Abstand aber auf der krummen Spirale gilt, źberschneiden sich die Kreise etwas, was vor allem im Zentrum gut sichtbar ist. Kreise mit ungeraden Nummern sind blau, Kreise mit geraden Nummern rot gefŠrbt.
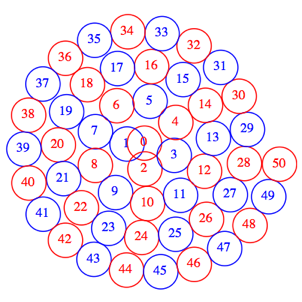
Abb. 2: Kreise und Zahlen
4 Quadrate
Wir ersetzen die Kreise durch Quadrate (Abb. 3). Wegen der Spiralenkrźmmung gibt es †berlappungen und Lźcken. Diese werden gegen au§en kleiner.
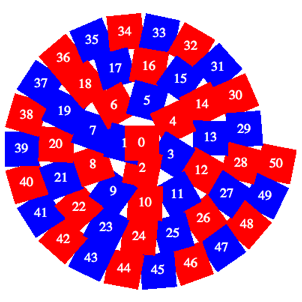
Abb. 3: Quadrate
Wir vergrš§ern die Anzahl der Quadrate und lassen die Nummern weg (Abb. 4).

Abb. 4: 2000 Quadrate
In der Abbildung 5 wurde die zyklische FŠrbung rot, gelb, blau verwendet.

Abb. 5: FŠrbung rot, gelb, blau
5 Quadratzahlen
In den Abbildungen 6 bis 8 sind die Quadratzahlen rot markiert, alle anderen Zahlen blau.
Wenn wir bis 169 gehen, erkennen wir zwei Spiralen, eine mit den geraden Quadratzahlen und eine mit den ungeraden Quadratzahlen (Abb. 6).
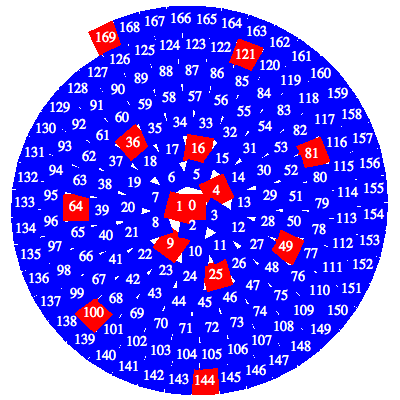
Abb. 6: Zwei Quadratzahlen-Spiralen
Wenn wir jedoch 2025 Quadrate zeichnen, erkennen wir 7 Quadratzahlen-Spiralen (Abb. 7, die Zahlen sind nicht angeschrieben). Warum gerade 7, ist mir nicht ersichtlich. Mšglicherweise haben wir es mit einer optischen TŠuschung zu tun.

Abb. 7: Quadratzahlen rot
In der Abbildung 8 sind die betreffenden Quadratzahlen beschriftet.
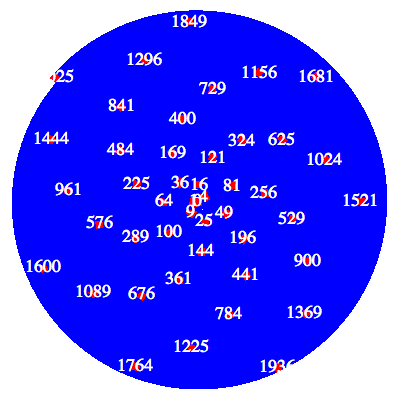
Abb. 8: Quadratzahlen
Die mit null beginnende Spirale enthŠlt die Zahlen:
|
Zahl |
0 |
49 |
196 |
441 |
784 |
1225 |
1764 |
|
Quadrat von |
0 |
7 |
14 |
21 |
28 |
35 |
42 |
Die mit eins beginnende Spirale enthŠlt die Zahlen:
|
Zahl |
1 |
64 |
225 |
484 |
841 |
1296 |
1849 |
|
Quadrat von |
1 |
8 |
15 |
22 |
29 |
36 |
43 |
Wir erkennen das Bildungsgesetz.
In der Abbildung 9 sind die Wurzeln direkt angegeben.
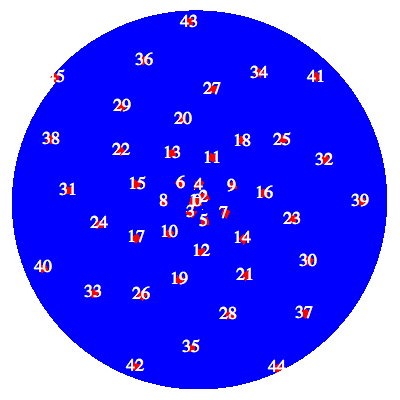
Abb. 9: Wurzeln
Wenn wir jetzt mit dem Finger den geraden Wurzeln nachfahren, also 0, 2, 4, 6, 8, 10, 12, 14, ... , bewegen wir uns wiederum auf einer Spiralen. Dasselbe gilt fźr die ungeraden Wurzeln.
Wer jetzt noch Lust hat, kann den Dreier-Wurzeln 0, 3, 6, 9, 12, 15, 18, 21, ... nachfahren.
6 Primzahlen
Wir fŠrben die Quadrate mit Primzahlnummern rot, die restlichen blau (Abb. 10). Es ist kein Muster erkennbar.

Abb. 10: Primzahlen rot