Hans Walser, [20160726]
Kegel im SchrŠgbild
1 Worum geht es?
Das Zeichnen eines geraden Kreiskegels im SchrŠgbild war frźher eine recht aufwŠndige Sache, da man fźr die Bodenellipse die Achsen aus konjugierten Durchmessern konstruieren musste (Verfahren von Rytz).
Mit DGS (der Autor verwendete GeoGebra) geht alles sehr rasch und einfach.
Es wird kleinschrittig das Zeichenverfahren vorgestellt.
2 Konstruktionsschritte
2.1 Umbeschriebenes Bodenquadrat
Das dem Bodenkreis umbeschriebene achsenparallele Quadrat sei im SchrŠgbild gegeben. Wir sehen also ein Parallelogramm mit zwei horizontalen Seiten (Abb. 1).

Abb. 1: Umbeschriebenes Bodenquadrat
2.2 Bodenkreis
Der Bodenkreis erscheint als dem Parallelogramm einbeschriebene Ellipse mit Berźhrung in den Seitenmitten. Dies ist die sogenannte Steiner-Ellipse des Parallelogramms.
Wir zeichnen nun die Seitenmitten und die Mittelparallelen des Bodenquadrates (Abb. 2). Zugleich setzen wir die Kegelhšhe mit Spitze ein.
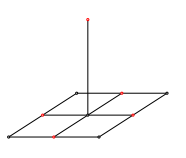
Abb. 2: Seitenmitten und Hšhe
Die gesuchte Ellipse geht durch die vier roten Seitenmitten. Da eine Ellipse erst durch fźnf Punkte bestimmt ist, suchen wir noch einen fźnften Punkt.
Wir zeichnen eine Halbdiagonale des Bodenquadrates und deren Mittelpunkt. Diesen Mittelpunkt strecken wir von der Quadratmitte aus mit dem Faktor sqrt(2) (Abb. 3).
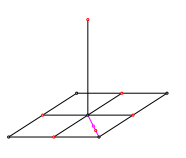
Abb. 3: Fźnfter Punkt
Nun kšnnen wir die Ellipse des Bodenkreises zeichnen (Abb. 4).
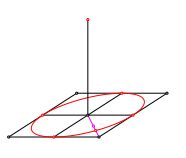
Abb. 4: Bodenkreis
Die Ellipse hat ăschrŠgeŇ Achsen und sieht unnatźrlich aus. Das SchrŠgbild ist halt eine schematische Zeichnung und entspricht nicht unseren Sehgewohnheiten.
Von der Kegelspitze aus zeichnen wir die Tangenten mit Berźhrungspunkten an die Ellipse (Abb. 5).
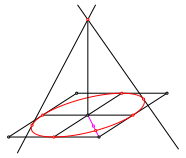
Abb. 5: Tangenten
So erhalten wir den Umriss des Kegels.
Abb. 6: Kegel
In der Abbildung 7 ist das Profildreieck in wirklicher Grš§e eingezeichnet. Dies ist nur im SchrŠgbild mšglich.

Abb. 7: Profildreieck