Hans Walser, [20180321a], [20180405]

Kegelaufgaben

Anregung: A. C., V. und K. H., Gö.

1 Worum geht es

Extremwertaufgaben mit der Kugel um- und einbeschriebenem Kegel. Vergleich mit Kugelvolumen.

2 Umbeschriebener Kegel

2.1 Aufgabe

Der Einheitskugel soll ein Kegel minimalen Volumens umbeschrieben werden.

2.2 Disposition

Die Abbildung 1 zeigt einen Achsenschnitt mit den benötigten Bezeichnungen.

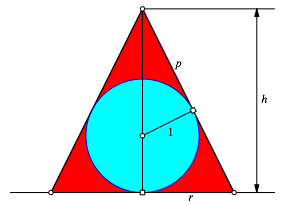
Abb. 1: Achsenschnitt

2.3 Bearbeitung

Wir verwenden die Kegelhöhe h als Parameter der Aufgabe.

Zunächst ist:

(1)

Weiter ist:

(2)

Für das Kegelvolumen V erhalten wir:

(3)

Zur Berechnung des Minimums leiten wir ab:

(4)

Nullsetzen der ersten Ableitung liefert die nichttriviale Lösung h = 4. Es ist dann:

(5)

Das minimale Kegelvolumen ist also das Doppelte des Inkugelvolumens.

Die Abbildung 2 zeigt die Lösung.

Abb. 2: Minimales Kegelvolumen

3 Eingeschriebener Kegel

3.1 Aufgabe

Der Einheitskugel soll ein Kegel maximalen Volumens einbeschrieben werden.

3.2 Disposition

Die Abbildung 3 zeigt einen Achsenschnitt mit den benötigten Bezeichnungen.

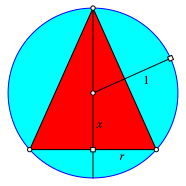
Abb. 3: Achsenschnitt

3.3 Bearbeitung

Wir verwenden x als Parameter der Aufgabe. Zunächst ist:

(6)

Für das Kegelvolumen V erhalten wir:

(7)

Zur Berechnung des Maximums leiten wir ab:

(8)

Nullsetzen der ersten Ableitung liefert für x die nichttriviale Lösung . Es ist dann

und (9)

Das maximale Kegelvolumen ist des Kugelvolumens.

Die Abbildung 4 zeigt die Lösung.

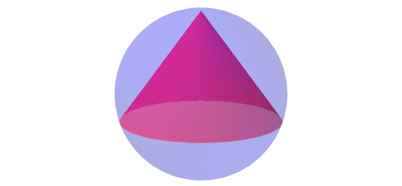
Abb. 4: Maximales Kegelvolumen

4 Link mit dem DIN-Format

Die Abbildung 5 zeigt die Achsenschnitte für die Extremlösungen im Vergleich mit dem DIN-Format (Walser 2013).

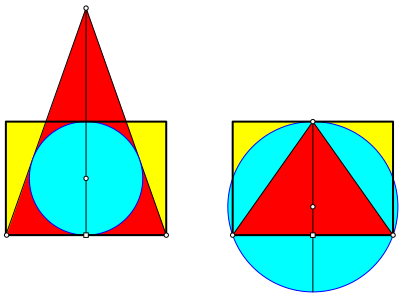
Abb. 5: Link mit dem DIN-Format

Literatur

Walser, H. (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.