Hans Walser, [20150919]

Kegelschnitte im Dreieck

1 Worum geht es?

Zu einem Dreieck studieren wir Kegelschnitte, welche zwei der drei Dreiecksecken als Brennpunkte haben und durch die dritte Ecke verlaufen.

Es entstehen interessante Schnittpunkte.

Ebenso erhalten wir die Berührungspunkte des Inkreises und der Ankreise mit den Dreiecksseiten.

2 Hyperbel

Zu einem Dreieck ABC zeichnen wir die Hyperbel, welche A und B als Brennpunkte hat und durch die Ecke C verläuft (Abb. 1).

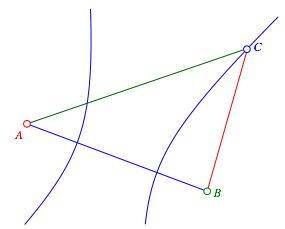
Abb. 1: Hyperbel

Nun wiederholen wir das Verfahren entsprechend für die Brennpunkte B und C sowie C und A (Abb. 2).

3 Schnittpunkte

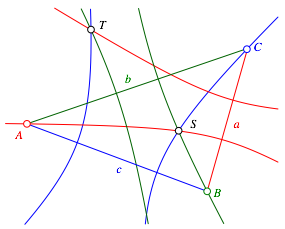
Abb. 2: Drei Hyperbeln

Wir stellen fest, dass die drei durch die Dreiecksecken verlaufenden Hyperbeläste einen Punkt S gemeinsam haben. Die drei anderen Hyperbeläste haben ebenfalls einen Punkt gemeinsam (T).

Beweis für S:

Blauer Hyperbelast: (1)

Roter Hyperbelast: (2)

Grüner Hyperbelast: (3)

Wir schneiden den blauen Hyperbelast mit dem roten Hyperbelast und nennen den Schnittpunkt S. Wegen (1) und (2) gilt:

(4)

Subtraktion der beiden Gleichungen liefert:

(5)

Damit erfüllt S die Gleichung (3) und liegt daher auch auf dem grünen Hyperbelast.

Für T geht der Beweis analog.

Die geometrische Bedeutung der beiden Schnittpunkte S und T wird im Abschnitt 6 besprochen.

4 Inkreis

Wir nehmen nun nur die drei durch die Ecken verlaufenden Hyperbeläste und schneiden sie mit der Gegenseite des Dreiecks (Abb. 3).

Wir stellen fest, dass diese drei Punkte , und die Berührungspunkte des Inkreises mit den Dreiecksseiten sind.

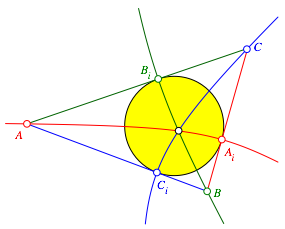
Abb. 3: Inkreis

Beweis: Wir führen die in der Dreiecksgeometrie übliche Abkürzung s als halben Umfang ein:

(6)

Da auf dem blauen Hyperbelast liegt, gilt nach (1):

(7)

Andererseits gilt:

(8)

Addition von (7) und (8) liefert:

(9)

Das ist aber genau der Tangentenabschnitt zum Inkreis. Analog für die übrigen Tangentenabschnitte.

5 Ankreise und Ellipsen

Wir nehmen nun den zweiten, nicht durch die Ecke A verlaufenden Ast der roten Hyperbel (Abb. 4) und weiter die Ellipse (blau) mit den Brennpunkten A und B durch C sowie die Ellipse (grün) mit den Brennpunkten C und A durch B und erhalten so die Berührungspunkte des Ankreises an die Seite a sowie zwei Schnittpunkte der drei Kegelschnitte.

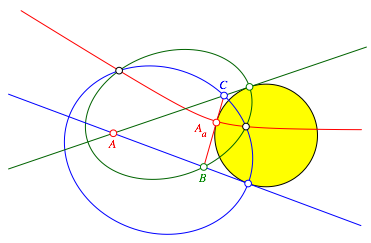
Abb. 4: Ankreis und weitere Schnittpunkte

Die übrigen Ankreise entsprechend.

Die Abbildung 5 gibt die integrale Figur.

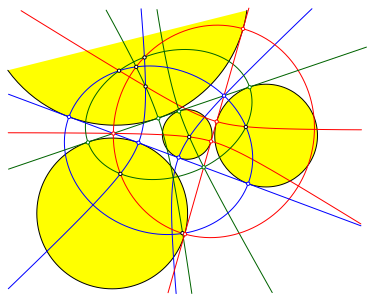
Abb. 5: Integrale Figur

6 Geometrische Bedeutung der Schnittpunkte

Da die beiden von einer Dreiecksecke ausgehenden Tangentenabschnitte an den Inkreis gleich lang sind, können wir die Abbildung 3 mit drei sich berührenden Kreisen ergänzen, welchen die Dreiecksecken als Zentren haben (hellblau in Abb. 6).

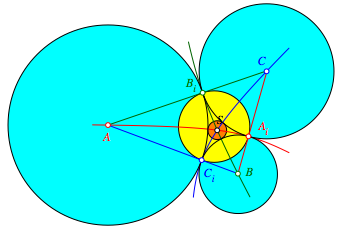
Abb. 6: Drei Kreise

Der Schnittpunkt S ist das Zentrum des Kreises, der diese drei hellblauen Kreise von außen berührt.

Beweis: Das Zentrum eines jeden Kreises, der die beiden hellblauen Kreise um A und um B von außen berührt, liegt auf dem blauen Hyperbelast. Dies folgt aus der Abstandsdefinition der Hyperbel. Entsprechend ist das Zentrum eines jeden Kreises, der die beiden hellblauen Kreise um B und um C von außen berührt, auf dem roten Hyperbelast. Daher hat der Kreis, der alle drei hellblauen Kreise von außen berührt, auf dem Schnittpunkt der Hyperbeläste.

Entsprechend ist T das Zentrum des Kreises, der die drei hellblauen Kreise umschließen berührt (Abb. 7).

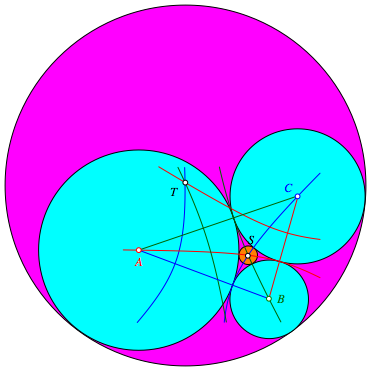
Abb. 7: Umschließende Berührung

Die Abbildung 8 zeigt die entsprechende Situation für den Fall eines Ankreises (vgl. Abb. 4). Die Kreise berühren teilweise von außen und teilweise von innen.

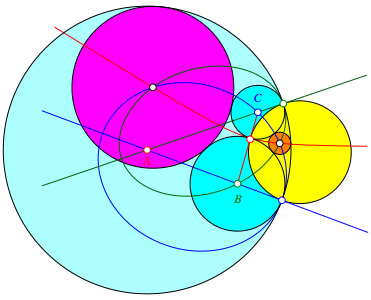
Abb. 8: Situation beim Ankreis

7 Eine Schließungsfigur

Wir starten mit einem beliebigen Bogen mit dem Zentrum in einer Dreiecksecke und fahren weiter gemäß Abbildung 9. Nach sechs Schritten schließt sich die Figur.

Abb. 9: Schließungsfigur

In der Mitte haben wir ein Bogendreieck.

Wenn wir den ersten Bogen durch den Schnittpunkt S legen, verschwindet dieses Bogendreieck. Wir erhalten eine Tropfenfigur um den Punkt S (Abb. 10). Der Kreis, der diese Figur umschließt, hat sein Zentrum in T.

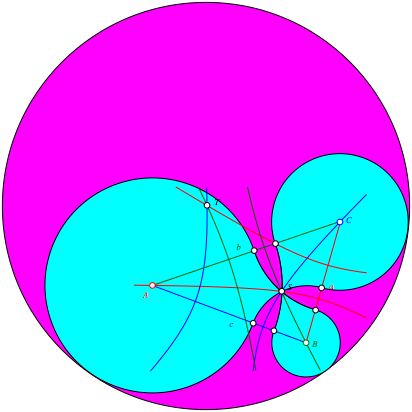
Abb. 10: Drei Tropfen