Hans Walser, [20150907]

Kegelschnitte und Tangentenvierecke

1 Worum geht es?

Wir können mit Kegelschnitten Tangentenvierecke zeichnen.

2 Hyperbel

Auf einem Hyperbelast mit den Brennpunkten F und G wählen wir zwei Punkte A und B. Das Viereck FAGB ist ein Tangentenviereck (Abb. 1).

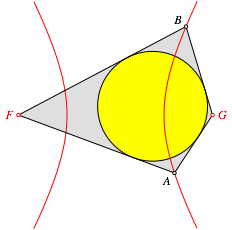
Abb. 1: Tangentenviereck

Das geht auch im nicht konvexen Fall (Abb. 2).

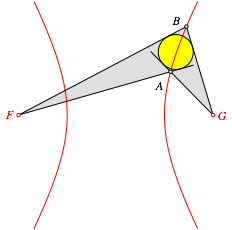
Abb. 2: Nicht konvexes Beispiel

3 Ellipse

Auf einer Ellipse mit den Brennpunkten F und G wählen wir zwei Punkte A und B. Das Viereck FAGB ist ein Tangentenviereck (Abb. 3).

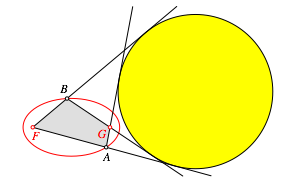
Abb. 3: Ankreis

Es geht auch im nicht konvexen Fall (Abb. 4).

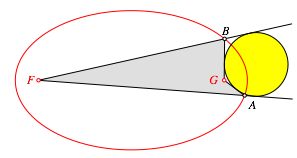
Abb. 4: Nicht konvexes Beispiel

Und es geht auch im „überschlagenen“ Fall (Abb. 5).

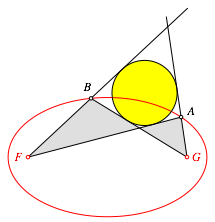
Abb. 5: Überschlagenes Tangentenviereck

Wir erkennen in der Abbildung 5 ein weiteres, konvexes Tangentenviereck. Die beiden noch nicht bezeichneten Ecken liegen auf einer Hyperbel mit den beiden Brennpunkten F und G (Abb. 6).

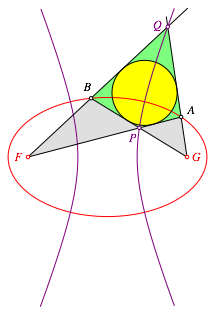
Abb. 6: Hyperbel

4 Diagonalkegelschnitte

Wir können die Sichtweise auch umkehren: wir beginnen mit einem Tangentenviereck ABCD und zeichnen die beiden weiteren Schnittpunkte F und G (Abb. 7).

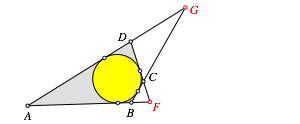
Abb. 7: Tangentenviereck

Dann liegen die beiden gegenüberliegenden Ecken A und C sowie B und D je auf einem Kegelschnitt mit den Brennpunkten F und G (Abb. 8). Wir erhalten zwei „Diagonalenschnittpunkte“ M und N.

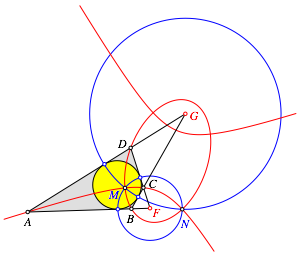
Abb. 8: Diagonale Kegelschnitte

Die Kreise um F beziehungsweise G durch die Berührungspunkte des Inkreises verlaufen ebenfalls durch M und N.

5 Parabel

Wir beginnen mit einer Parabel mit dem Brennpunkt F. Der Punkt G sei der unendlich ferne Punkt auf der Symmetrieachse der Parabel. Auf der Parabel wählen wir die beiden Punkte A und B. Das Viereck FAGB ist dann ein Tangentenviereck (Abb. 9).

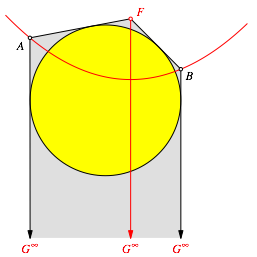
Abb. 9: Parabel

6 Hintergrund

Der Hintergrund dieser Eigenschaften sind die Abstandsdefinitionen der Kegelschnitte.