Hans Walser, [20091010a]
Kegelschnitte
Anregung: Chr. W., Z.
1 Worum geht es?
Wenn wir bei der klassischen Abstandsdefinition der Parabel mit Leitgerade und Brennpunkt die Leitgerade durch einen Kreis ersetzen, erhalten wir eine Ellipse oder eine Hyperbel, je nachdem, ob der Brennpunkt im Innern oder im €u§ern des Kreises liegt. Die Frage ist nun, was beim †bergang von der Ellipse zur Hyperbel geschieht. Je nach dem Design der Konstruktion kann das eine Parabel oder eine Halbgerade sein.
2 Leitlinien
2.1.1 Leitgerade
Die Menge aller Punkte, welche von einer Geraden l und einem Punkt F denselben Abstand haben, ist eine Parabel mit dem Brennpunkt F.
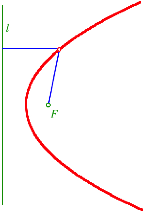
Abstandsdefinition der Parabel
2.1.2 Leitkreis
Wir ersetzen nun die Gerade l durch einen Kreis k mit dem Mittelpunkt M und dem Radius r. Wenn F im Innern von k liegt, erhalten wir mit der entsprechenden Abstandsdefinition eine Ellipse, andernfalls eine Hyperbel, wobei aber nur ein Hyperbelast relevante ist. Der zweite Brennpunkt ist M, die Abstandssumme beziehungsweise Abstandsdifferenz von den beiden Brennpunkten ist r.
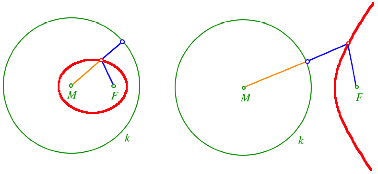
Ellipse und Hyperbel
3 †bergang
Wir fragen nun nach der †bergangsfigur zwischen Ellipse und Hyperbel.
3.1 Fester Leitkreis, variabler Brennpunkt
Wenn der Brennpunkt F auf dem Leitkreis k liegt, ist die durch die Abstandsdefinition gegebene Ortslinie der Strahl von M durch F.
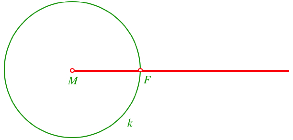
†bergangsfigur ein Strahl
Wir erhalten keine Parabel. — Jedenfalls nicht als Scharkurve.
Wenn wir allerdings den Punkt F auf einer Geraden durch den Kreismittelpunkt M bewegen und die zugehšrige Kegelschnittschar zeichnen, sehen wir als Enveloppe zwei quadratische Parabeln.
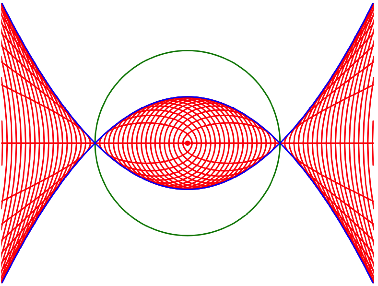
Enveloppe besteht aus zwei Parabeln
3.2 Fester Brennpunkt, variable Kreise
Wir halten nun den Brennpunkt fest und arbeiten mit Kreisscharen. Diese generieren wir auf zwei unterschiedliche Arten.
3.2.1 Kreisbźschel
Wir arbeiten mit einem Kreisbźschel durch die beiden Punkt A und B. Den Brennpunkt F wŠhlen wir fest auf der Mittelsenkrechten der Strecke AB. Wir erhalten Ellipsen, als †bergangskurve eine Parabel, sowie Hyperbeln. Alle Kurven sind tangential an die Mittelsenkrechten von FA und FB. Diese bilden die Enveloppe der Kurvenschar.
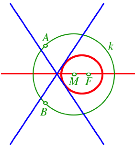
Ellipse
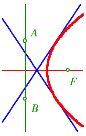
Parabel
Bei der Parabel ist der Mittelpunkt M des ăKreisesŇ im Unendlichen.
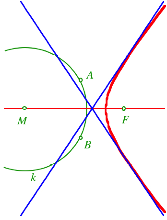
Hyperbel
3.2.2 Apolloniuskreise
3.2.2.1 Die drei Kegelschnitte
Zur gegebenen Strecke FG sei U ein innerer und V der zugehšrige Šu§ere Teilpunkt, k der Thaleskreis źber der Strecke UV, also der Apolloniuskreis zur Strecke FG zum durch U definierten TeilverhŠltnis. Falls U nŠher bei F liegt, erhalten wir eine Ellipse.
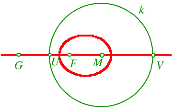
Ellipse
Ist U der Mittelpunkt der Strecke FG, wird der Apolloniuskreis zur Mittelsenkrechte dieser Strecke, und wir erhalten als †bergangsfigur die Parabel.
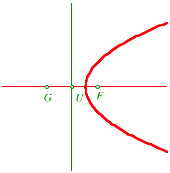
Parabel
Ist schlie§lich U nŠher bei G, ergibt sich eine Hyperbel. Es ist nur ein Hyperbelast relevant.
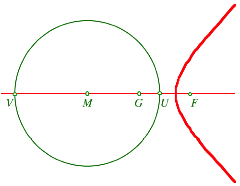
Hyperbel
3.2.2.2 Der zweite Hyperbelast
In der folgenden Figur ist die Parabel gezeichnet, zusŠtzlich der Apolloniuskreis k, welcher zu einem Punkt U nŠher bei F gehšrt. Dann ist links in der Figur der Hyperbelast gezeichnet, der aus den Punkten mit gleichen AbstŠnden vom Kreis k und dem Brennpunkt G besteht. Schlie§lich ist auch noch der zugehšrige zweite Hyperbelast gezeichnet. Dieser Hyperbelast, die Parabel und der Kreis k haben zwei gemeinsame Schnittpunkte.
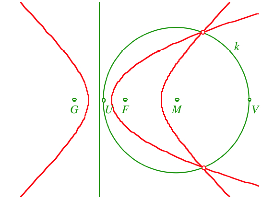
Gemeinsame Schnittpunkte