Hans Walser, [20201006], [20221113]
Kegelschnitte und Thaleskreise
Anregung: Zvonimir Durcevic, Wien
1 Worum gehrt es?
Spiel mit Kegelschnitten, Thaleskreisen und verschiedenen Berührungen.
Verifikationen mit DGS.
2 Ellipse
Wir beginnen mit einer Ellipse mit den Brennpunkten F1 und F2 und einem Ellipsenpunkt P (Abb. 1.1). Wir zeichnen auch die Ellipsenachse durch die beiden Brennpunkte.
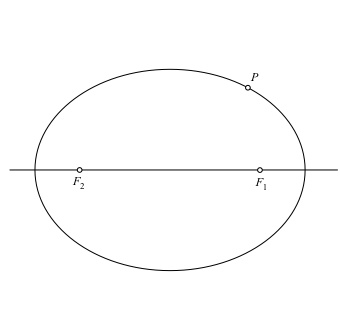
Abb. 1.1: Ellipse
Nun zeichnen wir den Thaleskreis über den spitzen Scheiteln S1 und S2 (blau in Abb. 1.2).

Abb. 1.2: Thaleskreis über spitzen Scheiteln
Weiter zeichnen wir die Thaleskreise über den Strecken F1P und F2P (rot in Abb. 1.3). Die Summe der Radien der beiden roten Kreise ist gleich dem Radius des blauen Kreises (Abstandseigenschaft der Ellipse).
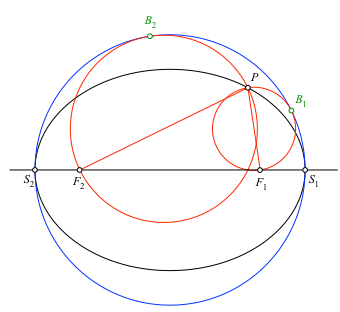
Abb. 1.3: Thaleskreise
Und nun wird es spannend: die beiden roten Kreise berühren den blauen Kreis von innen. Verifikation mit DGS.
Die Gerade durch die beiden Berührpunkte B1 und B2 ist die Tangente an die Ellipse im Ellipsenpunkt P (Abb. 1.4). Verifikation mit DGS.
Die Strecken F1B1 und F2B2 sind senkrecht zur Ellipsentangente (Thaleskreise).
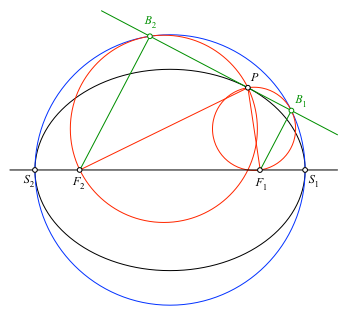
Abb. 1.4: Ellipsentangente
Und noch ein kleiner Nachbrenner: der zweite Schnittpunkt G der beiden roten Kreise liegt auf der Ellipsenachse. Die Strecke GP ist senkrecht zur Ellipsenachse (Abb. 1.5). Verifikation mit DGS.
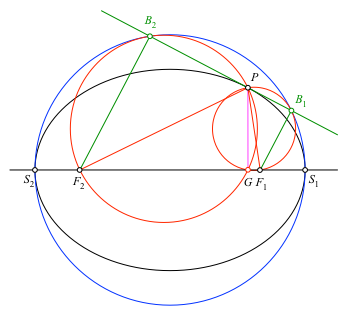
Abb. 1.5: Schnittsehne der beiden roten Kreise
Die Animation 1.1 illustriert die Sachverhalte.
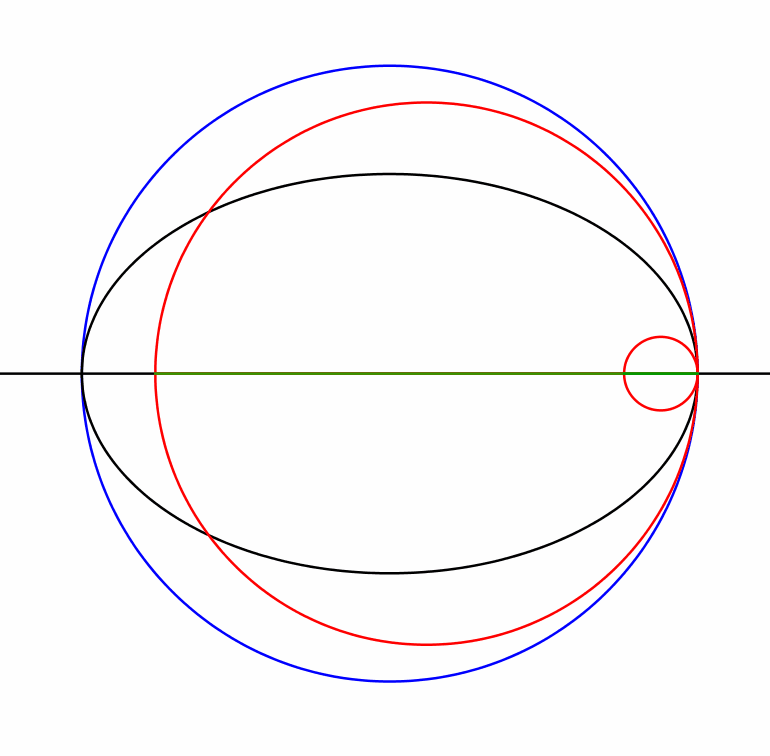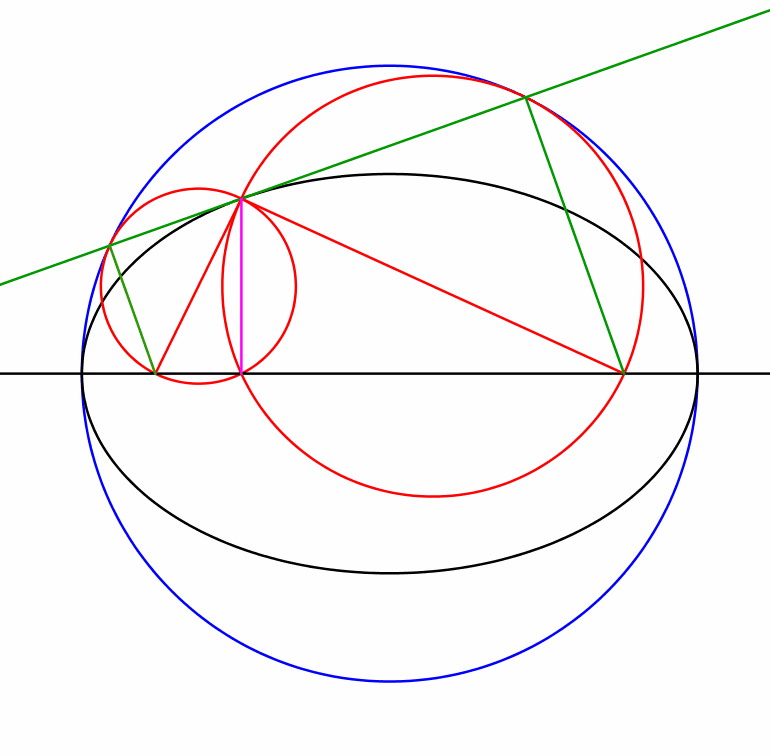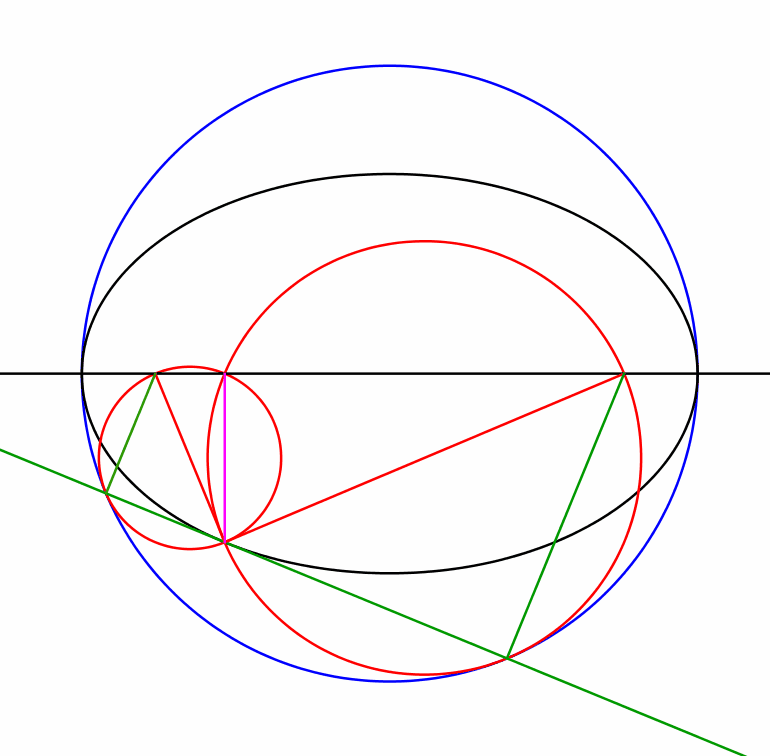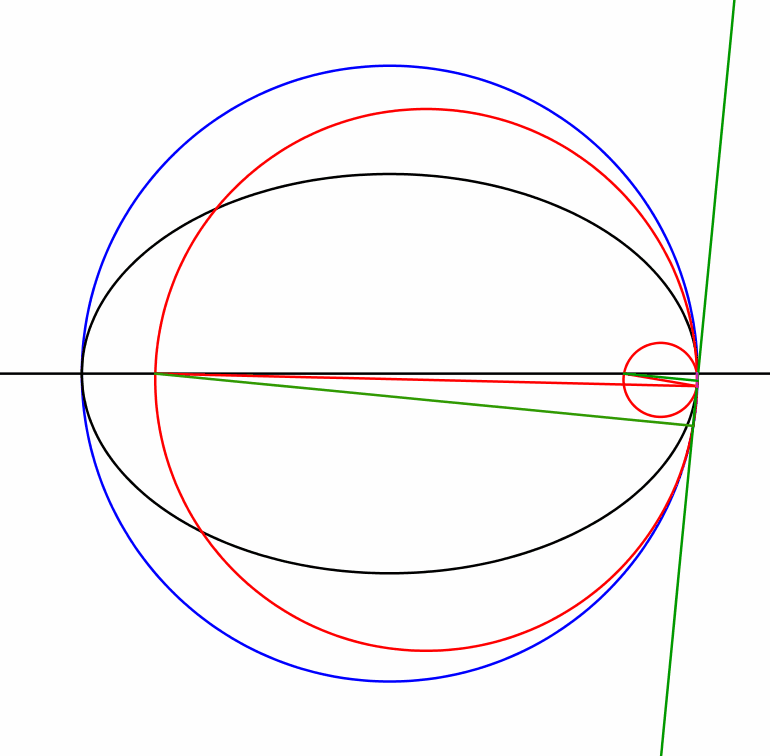
Animation 1.1: Ellipse und Thaleskreise
Der Mittelpunkt eines roten Kreises beschreibt ebenfalls eine Ellipse (Animation 1.2). Sie ist perspektivähnlich zur schwarzen Ellipse.
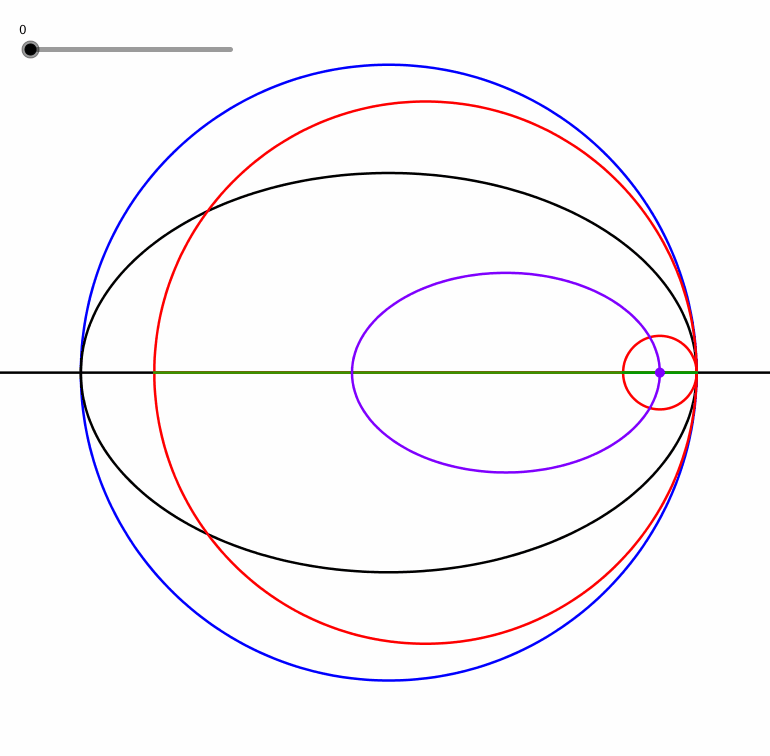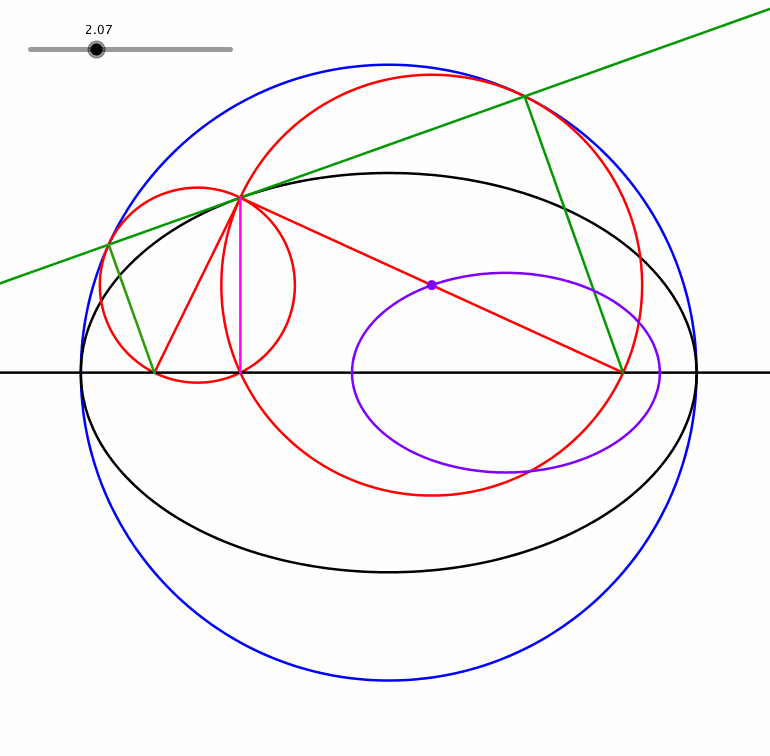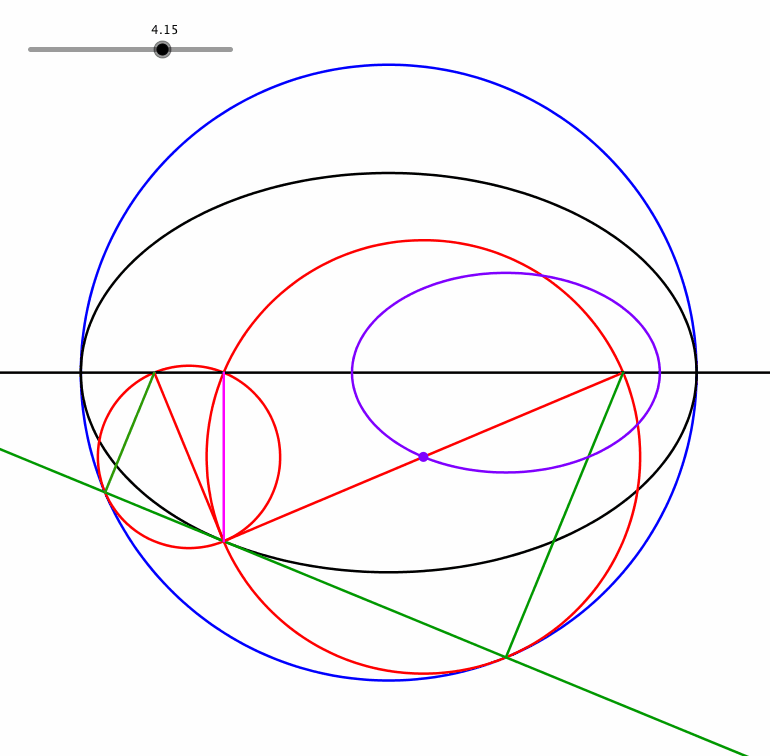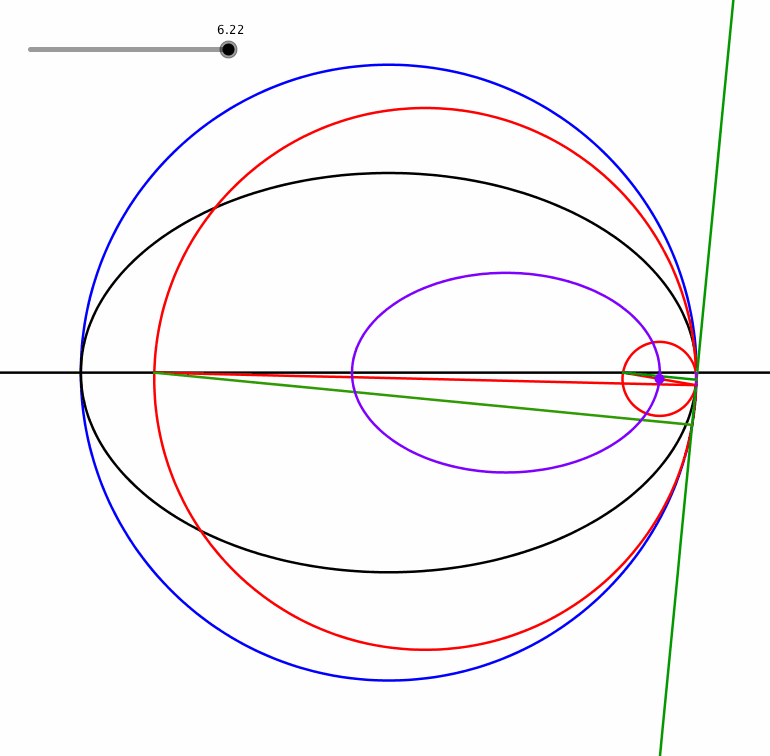
Animation 1.2: Perspektivähnliche Ellipse
Ein Punt zwischen dem Mittelpunkt und dem grünen Eckpunkt beschreibt eine eiförmige Kurve (Animation 1.3).
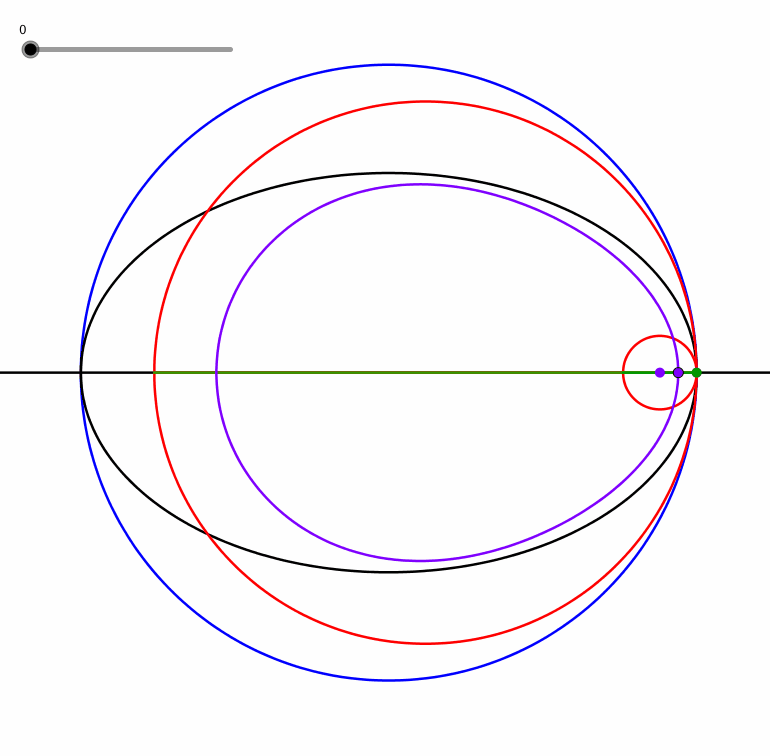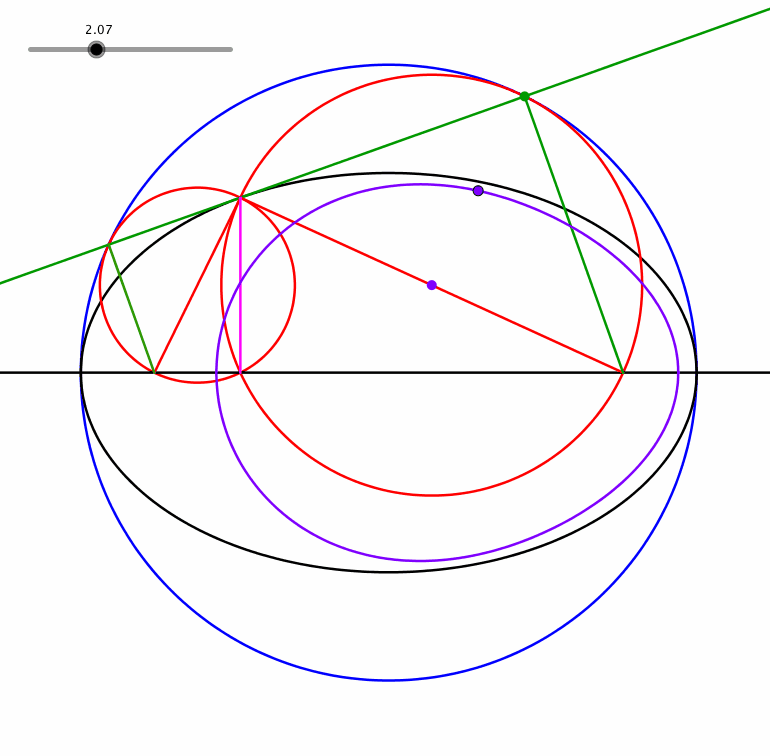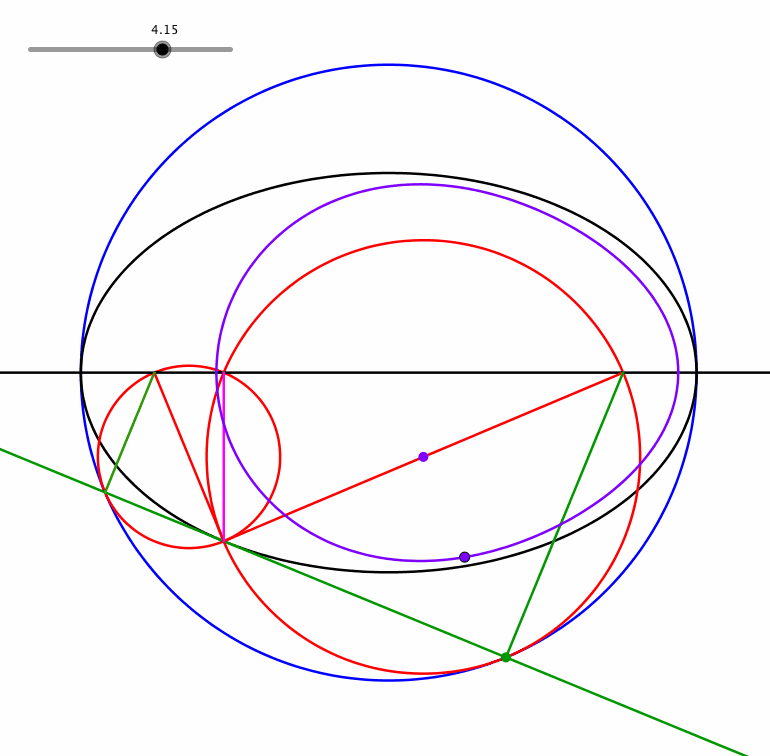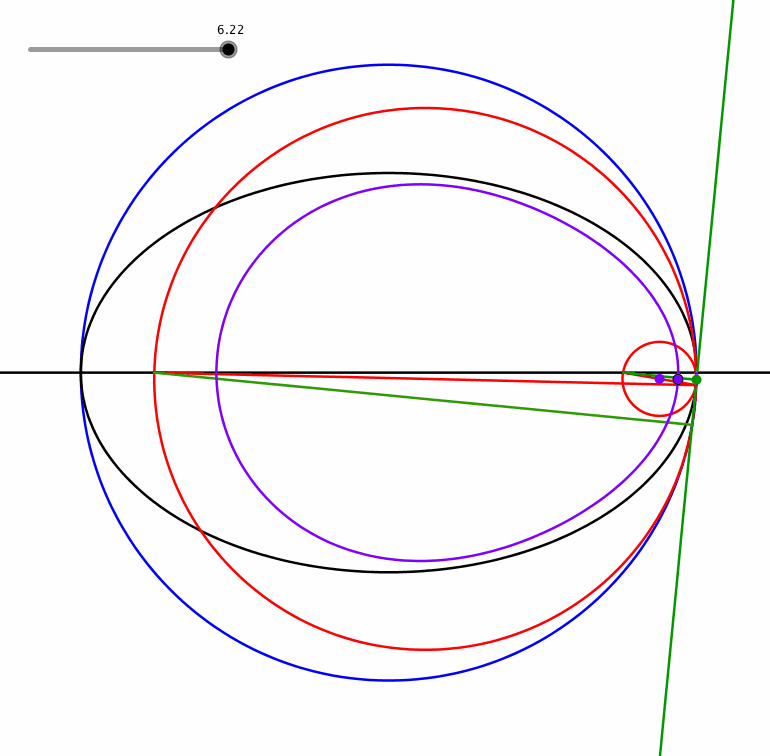
Animation 1.3: Eiförmige Kurve
Ein Punkt auf der anderen Seite führt zu einer Dreiblattschlinge (Animation 1.4).
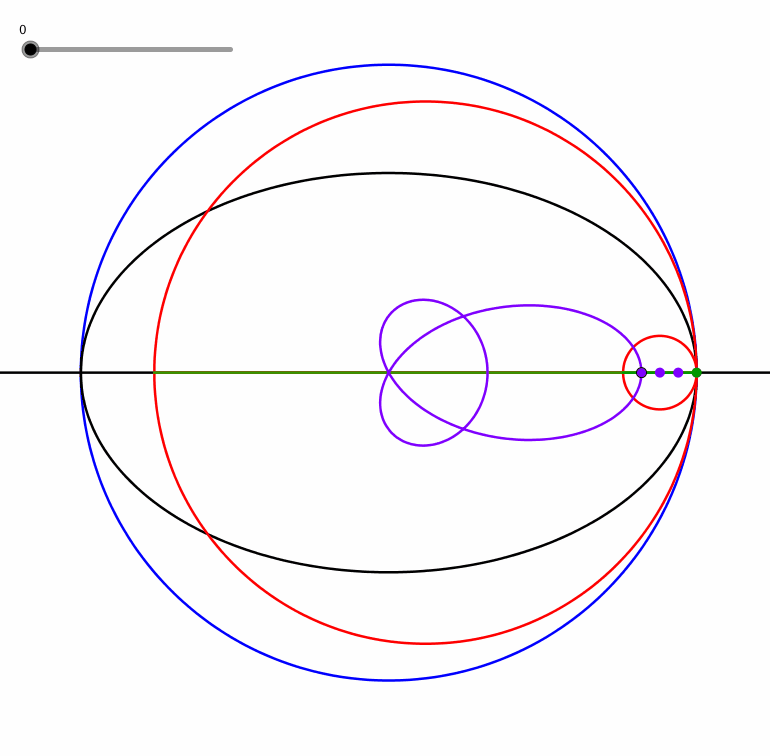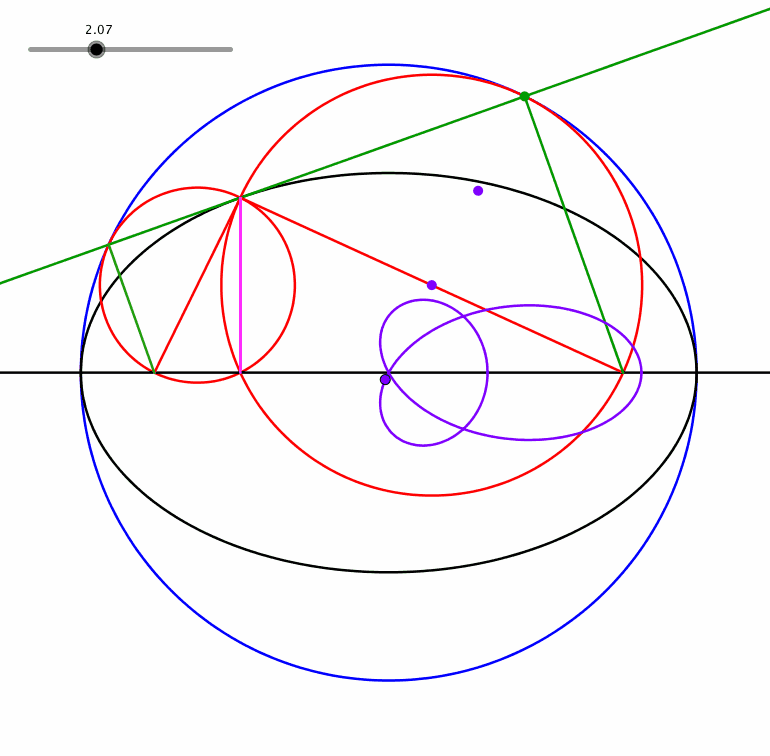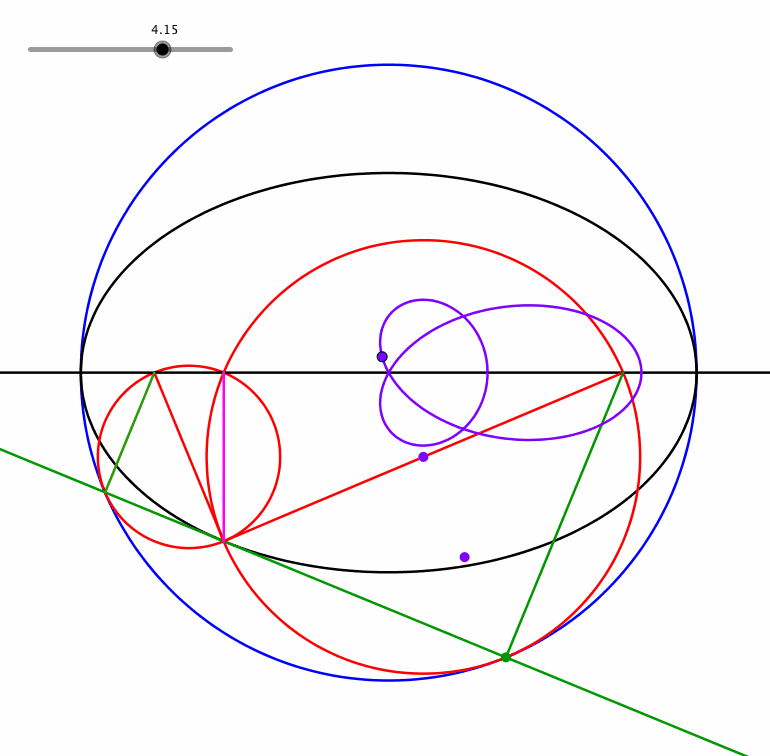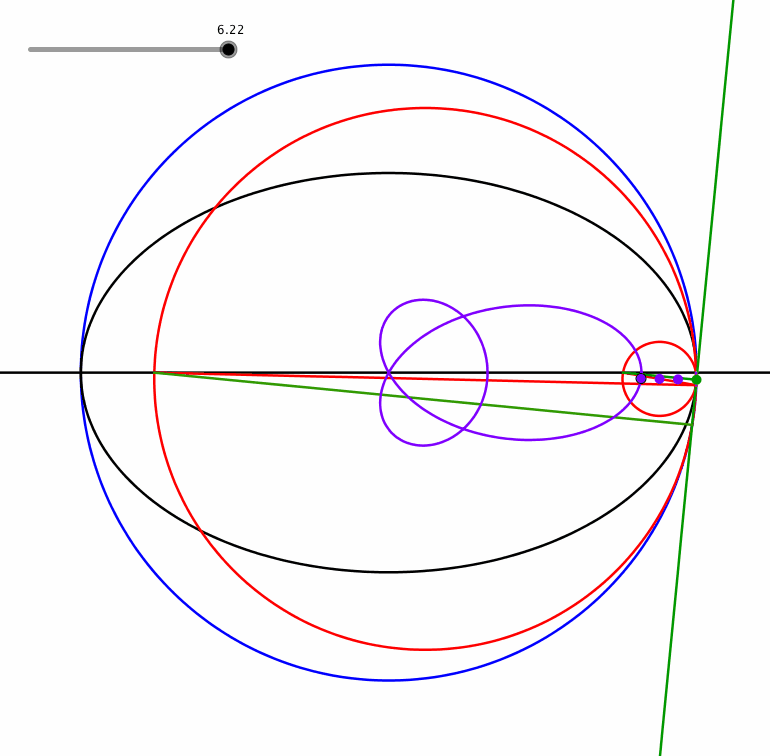
Abb. 1.4: Dreiblattschlinge
3 Hyperbel
Bei der Hyperbel läuft es analog. Wir beginnen mit einer Hyperbel mit den Brennpunkten F1 und F2 und einem Hyperbelpunkt P (Abb. 2.1). Wir zeichnen auch die Hyperbelachse durch die beiden Brennpunkte.

Abb. 2.1: Hyperbel
Nun zeichnen wir den Thaleskreis über den Scheiteln S1 und S2 (blau in Abb. 2.2).
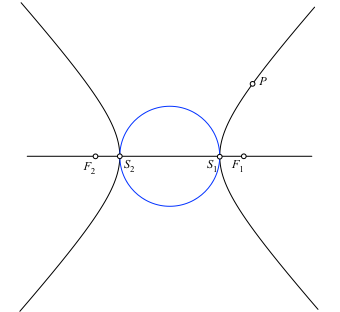
Abb. 2.2: Thaleskreis über Scheiteln
Weiter zeichnen wir die Thaleskreise über den Strecken F1P und F2P (rot in Abb. 2.3). Die Differenz der Radien der beiden roten Kreise ist gleich dem Radius des blauen Kreises (Abstandseigenschaft der Hyperbel).
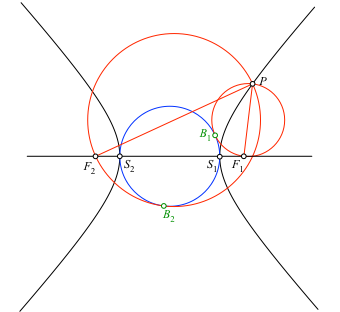
Abb. 2.3: Thaleskreise
Und nun wird es spannend: die beiden roten Kreise berühren den blauen Kreis von außen. Verifikation mit DGS.
Die Gerade durch die beiden Berührpunkte B1 und B2 ist die Tangente an die Hyperbel im Hyperbelpunkt P (Abb. 2.4). Verifikation mit DGS.
Die Strecken F1B1 und F2B2 sind senkrecht zur Hyperbeltangente (Thaleskreise).

Abb. 2.4: Hyperbeltangente
Und wieder ein kleiner Nachbrenner: der zweite Schnittpunkt G der beiden roten Kreise liegt auf der Hyperbelachse. Die Strecke GP ist senkrecht zur Hyperbelachse (Abb. 2.5). Verifikation mit DGS.

Abb. 2.5: Schnittsehne der beiden roten Kreise
4 Parabel
Bei der Parabel wird es einfacher. Wir beginnen mit einer Parabel mit dem Brennpunkt F und der Leitlinie l (Abb. 3.1). Weiter sei P ein Parabelpunkt. Ebenso zeichnen wir die Symmetrieachse.

Abb. 3.1: Parabel
Wir zeichnen die Scheiteltangente (blau in Abb. 3.2).
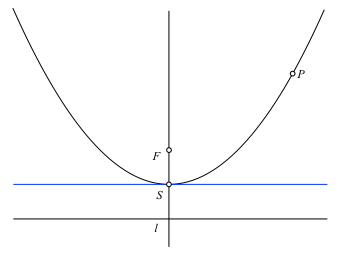
Abb. 3.2: Scheiteltangente
Nun zeichnen wir über der Strecke FP den Thaleskreis (rot in Abb. 3.3).
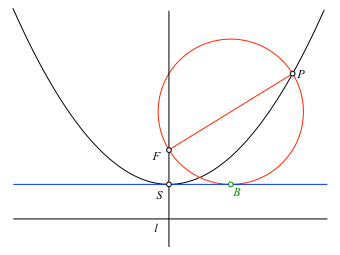
Abb. 3.3: Thaleskreis
Der Thaleskreis berührt die Scheiteltangente (Abb. 3.3). Dies folgt aus der Leitlinienkonstruktion der Parabel.
Die Parabeltangente in P verläuft durch den Berührungspunkt B (Abb. 3.4). Die Strecke FB ist senkrecht zur Parabeltangente.
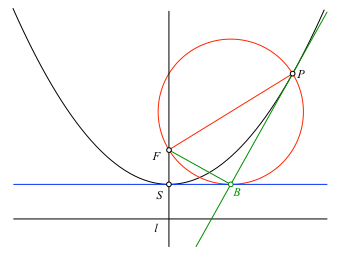
Abb. 3.4: Parabeltangente