Hans Walser, [20150214]
Kegelverdoppelung
1 Worum geht es?
Wenn wir bei einem Kegel die Hšhe verdoppeln, verdoppelt sich auch das Volumen. Wie lŠsst sich das durch Cavalieri-Zerlegung zeigen?
Bonaventura Cavalieri (1598-1647)
2 Cavalieri
Es werden drei Varianten des Cavalieri-Prinzips vorgestellt.
Wir arbeiten jeweils mit zwei kongruenten Kegeln (rot und blau), welche volumenmŠ§ig ãaddiertÒ werden sollen.
Die Cavalieri-Zerlegung wird meist erst im Achsenschnitt sichtbar und verstŠndlich.
2.1 Kreisscheiben
Die beiden Kegel werden in horizontale Scheiben zerlegt. Der Scheibenradius nimmt linear mit der Positionshšhe der Scheibe ab.
Grundvorstellung: Scheiben einer runden Frucht, etwa Apfelscheiben, Ananasscheiben ohne Loch.
Die Scheiben der beiden Kegel werden nun im Wechsel neu aufeinander geschichtet. Es entsteht ein doppelt so hoher Kegel mit gleicher GrundflŠche.
Die Abbildungen 1, 2 und 3 zeigen Ansicht, Frontalansicht und Achsenschnitt.
Abb. 1: Scheiben
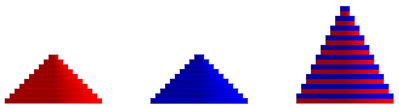
Abb. 2: Frontalansicht
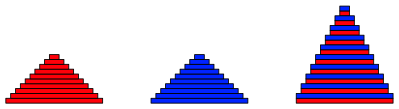
Abb. 3: Achsenschnitt
Das Verfahren funktioniert entsprechend fŸr die Addition von drei oder mehr Kegeln.
2.2 Hohlzylinder
Die beiden Kegel werden in ineinandergeschobene Hohlzylinder zerlegt. Die Hohlzylinderhšhe nimmt linear mit dem Radius ab.
Grundvorstellung: Kartonrolle einer aufgebrauchten WC-Rolle.
€u§erlich besteht kein Unterschied zur Zerlegung in Scheiben.
FŸr die Volumenaddition werden die Hohlzylinder des blauen Kegels Ÿber die Hohlzylinder des roten Kegels gestŸlpt. Der rote Kegel bleibt also unverŠndert, verschwindet aber fast vollstŠndig im Innern des Summenkegels.
Die Abbildungen 4, 5 und 6 zeigen Ansicht, Frontalansicht und Achsenschnitt.
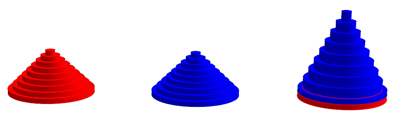
Abb. 4: Hohlzylinder
Abb. 5: Frontalansicht
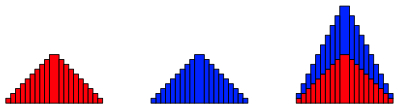
Abb. 6: Achsenschnitt
Das Verfahren funktioniert entsprechend fŸr die Addition von drei oder mehr Kegeln.
2.3 Hohlkegel
Die beiden Kegel werden in Hohlkegel zerlegt. Hšhe und Radius der Hohlkegel sind linear.
Grundvorstellung: KartonhŸtchen bei ãWer schnappt den HutÒ.
FŸr die Volumenaddition werden die Hohlkegel des blauen Kegels in umgekehrter Reihenfolge Ÿber den roten Kegel gestŸlpt. Der rote Kegel bleibt unverŠndert, verschwindet aber fast vollstŠndig im Innern des Summenkegels.
Die Abbildungen 7, 8 und 9 zeigen Ansicht, Frontalansicht und Achsenschnitt.
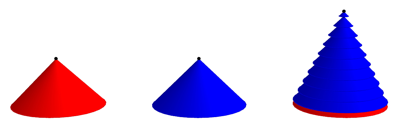
Abb. 7: Hohlkegel
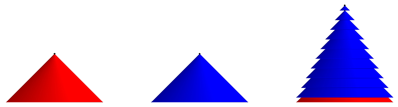
Abb. 8: Frontalansicht
Abb. 9: Achsenschnitt
Das Verfahren funktioniert auch fŸr die Addition von drei oder mehr Kegeln (Abb. 10 und 11).
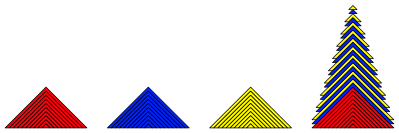
Abb. 10: Addition von drei Kegeln
Abb. 11: Pagode
3 Was leistet die Cavalieri-Zerlegung
3.1 Volumina
Die Cavalieri-Zerlegung ist keine echte geometrische Zerlegung, sondern lediglich eine Approximation der Volumina. Sie ist nur fŸr VolumenŸberlegungen brauchbar.
3.2 OberflŠchen
FŸr die OberflŠchenberechnung liefert die Cavalieri-Zerlegung falsche Resultate, wie das folgende Beispiel zeigt.
Ein Kegel mit dem Radius r und der Hšhe h hat die MantelflŠche (ohne GrundflŠche):
Wenn wir nun etwa mit der Scheiben-Zerlegung (Abb. 1) arbeiten, erhalten wir fŸr die ãMantelflŠcheÒ (ohne die GrundflŠche):
Dabei ist
der Summand 
der
waagerechte Anteil (Sonnenterrasse) der ãMantelflŠcheÒ.
Es ist 
. Die falsche Gleichsetzung von 
mit 
ist ein
klassischer SchŸlerfehler (kommt auch bei Mathematikdoktoranden vor).
4 Modellbau
Scheibenmodelle aus Holz oder Kunststoff lassen sich einfach herstellen. Damit die Scheiben nicht seitlich abrutschen, werden sie in der Mitte gelocht und auf einen Dorn aufgeschichtet. Dabei besteht eine gewisse Verletzungsgefahr.
Hohlzylinder und Hohlkegel sind ohne technische Hilfsmittel schwierig herzustellen.
Statt fŸr Kreiskegel kšnnen die †berlegungen auch fŸr Pyramiden gemacht werden. Die benštigten Hohlquader sind einfach herzustellen. Mit etwas Geschick und Geduld kšnnen auch Hohlpyramiden hergestellt werden.