Hans Walser, [20090626a]
Kehrzahl aus Gelenkmodell
1
Worum es geht
Wir untersuchen ein
Gelenkmodell, das zu einer Zahl deren Kehrzahl liefert. Es entstehen Trapeze,
insbesondere das goldene Trapez, welches die Zahlen 
, 
sowie 
in der Form des
goldenen Schnittes enthŠlt.
2 Das Gelenkmodell
Das Gelenkmodell
besteht aus je zwei StŠben der LŠnge eins und 
, die wechselseitig an den Enden gelenkig verbunden sind.
Damit kšnnen ein Rechteck im DIN-Format gebildet werden, oder Parallelogramme
mit dem SeitenverhŠltnis 
.
DIN-Rechteck und
Parallelogramm
Wir kšnnen die StŠbe
der LŠnge 
aber auch
Ÿberkreuzen. So kšnnen wir als Sonderfall das Quadrat bilden oder allgemein ein
gleichschenkliges Trapez.
Quadrat und Trapez
Damit das Modell
beweglich bleibt, darf die †berkreuzungsstelle nicht fixiert werden.
Wir werden nun diese
gleichschenkligen Trapeze untersuchen.
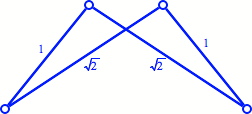
Das Gelenkmodell
3
Die Parallelseiten
Wir fragen zunŠchst,
wie sich die LŠngen der beiden Parallelseiten des gleichschenkligen Trapezes
zueinander verhalten.
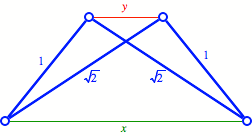
Parallelseiten
Gesucht ist also die
Funktion 
.
4
Die Rechnung
Wir zeichnen die
Symmetrieachse des Trapezes sowie eine Hšhe gemŠ§ Figur ein.
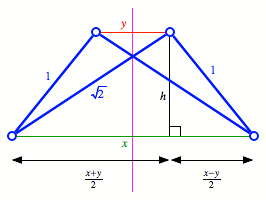
Symmetrieachse und Hšhe
Nach dem Satz des
Pythagoras gilt:
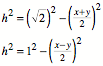
Daraus erhalten wir:
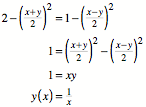
Somit ist y die Kehrzahl von. Die durch das GerŠt definiert
Funktion 
hat den
Definitionsbereich 
.
5
SonderfŠlle
5.1
Quadrat
Der Sonderfall des
Quadrates wurde schon erwŠhnt. Das Quadrat hat den kleinsten Umfang und die
grš§te FlŠche im Vergleich zu den anderen Trapezen.
Allgemein hat das
Trapez den Umfang:
Diese Funktion hat ihr
Minimum bei 
.
FŸr den FlŠcheninhalt 
verwenden wir
den Schnittwinkel 
zwischen den
Diagonalen. Der FlŠcheninhalt eines Viereckes ist allgemein die HŠlfte des Produktes
der beiden Diagonalen mit dem Sinus des Zwischenwinkels. In unserem Fall wird:
Das Maximum ist fŸr 
, also fŸr das Quadrat.
5.2
Goldenes Trapez
FŸr 
ist 
(goldener
Schnitt); wir erhalten das so genannte goldene Trapez.
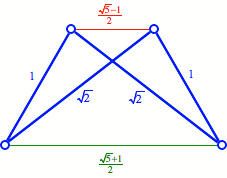
Goldenes Trapez
Wegen 
erhalten wir fŸr
das goldene Trapez die Hšhe:
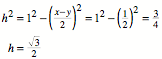
Das ist die Hšhe im
regulŠren Einheitsdreieck. Wir kšnnen dieses geeignet ins goldene Trapez
einpassen. Das goldene Trapez hat also die Basiswinkel 60¡.
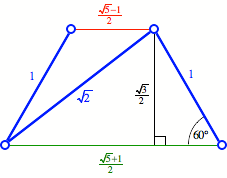
Ma§e und Winkel im
goldenen Trapez
Das goldene Trapez ist
wohl die einfachste Figur, welche 
, 
und 
enthŠlt. Dies ist umso verblŸffender, als 
vor allem in der
Geometrie des Quadrates auftritt, 
in der Geometrie
des regulŠren Dreieckes und 
in der Form des
goldenen Schnittes in der Geometrie des regulŠren FŸnfeckes. Diese Figuren
ãbei§enÒ sich aber. Dreieck und FŸnfeck lassen sich nicht in den Quadratraster
einfŸgen, und Quadrat und FŸnfeck lassen sich nicht in den Dreiecksraster
einfŸgen.
6
Verallgemeinerung
Wir wŠhlen die LŠngen
der StŠbe b und c mit 
. Damit kšnnen wir als Sonderfall ein Rechteck mit den Seiten
a und b mit 
bilden.
FŸr das
gleichschenklige Trapez fragen wir nach dem Zusammenhang der LŠngen der beiden
Parallelseiten.
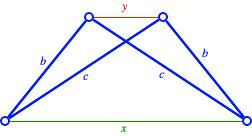
Verallgemeinerung
Nach EinfŸhren der Hšhe
h gilt:
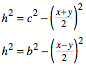
Daraus erhalten wir:
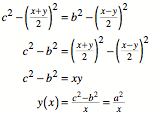
Im Prinzip wieder eine
Kehrwertfunktion.