Hans Walser, [20190809]
Kettenantrieb
1 Velokette
Eine Velokette ist genau besehen ein gleichseitiges Polygon. Die SeitenlŠnge ist die technische LŠnge eines Kettengliedes, in der Regel 1/2Ň (12.7mm) (Abb. 1). Entsprechend sind die zugehšrigen ZahnrŠder regelmŠ§ige Vielecke gleicher SeitenlŠnge.

Abb. 1: Gleichseitiges Polygon. SeitenlŠnge ½Ň
Die SeitenlŠnge ½Ň war auch der Lochabstand der historischen Metallbaukasten im letzten Jahrhundert.
2 Zwei gleiche ZahnrŠder
Wir normieren die technische LŠnge eines Kettengliedes und damit die SeitenlŠnge der regelmŠ§igen Vielecke auf 1.
2.1 Dreieckige ZahnrŠder
Die Abbildung 2 zeigt zwei gleichgerichtete dreieckige ZahnrŠder.
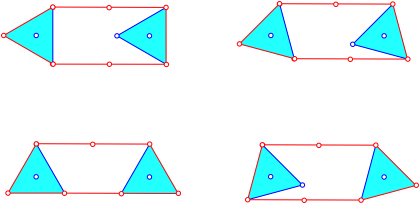
Abb. 2: Dreieckige ZahnrŠder
Beim Drehen der ZahnrŠder entstehen Parallelogramme. Der Abstand zwischen dem oberen und dem unteren Kettenteil verŠndert sich.
Die Abbildung 3 zeigt eine andere Anordnung.

Abb. 3: Andere Anordnung
Wenn wir die beiden Dreiecke drehen, verŠndern sich die orange eingezeichneten Strecken gemŠ§ Tabelle 1. Die orangen Strecken werden kźrzer. Die Kette wźrde bei konstantem Achsabstand der beiden dreieckigen ZahnrŠder durchhŠngen.
|
Drehwinkel |
LŠnge orange Strecke |
|
0ˇ |
2 |
|
15ˇ |
1.98596 |
|
30ˇ |
1.94420 |
Tab. 1: Orange Strecken
2.2 Viereckige ZahnrŠder
Die Abbildung 4 zeigt die Situation mit quadratischen ZahnrŠdern. Wir haben durchgehend Parallelogramme. Der Abstand zwischen dem oberen und dem unteren Kettenteil variiert.
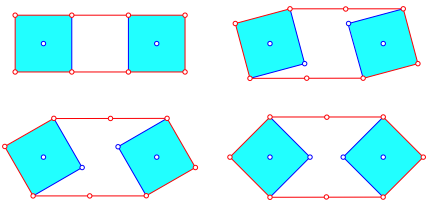
Abb. 4: Quadratische ZahnrŠder
Die beigefźgte Animation illustriert den Fall mit hexagonalen ZahnrŠdern.
Allgemein haben wir bei einer ungeraden Eckenzahl der regelmŠ§igen Vielecke das Problem wie bei den Dreiecken. Bei einer geraden Eckenzahl tritt dieses Problem nicht auf.
3 Ungleiche ZahnrŠder
Fźr eine †bersetzung benštigen wir zwei ZahnrŠder ungleicher Grš§e. Wir arbeiten exemplarisch mit dem einfachsten Fall eines quadratischen und eines dreieckigen Zahnrades. Die Abbildung 5 zeigt zwei Positionen eines Getriebes mit der KettenlŠnge 8. Eine Drehung um 45ˇ beim Quadrat fźhrt zu einer Drehung um 60ˇ beim Dreieck. Drei vollen Drehungen des Quadrates entsprechen vier volle Drehungen des Dreiecks.
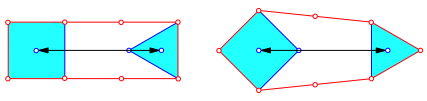
Abb.5: †bersetzung
Nun ist es aber so, dass bei diesen beiden Positionen der Achsabstand zwischen den ZahnrŠdern ungleich ist.
Fźr die Position links berechnen wir den Achsabstand:
![]() (1)
(1)
Fźr die Position rechts berechnen wir den Achsabstand:
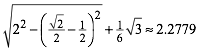 (2)
(2)
Bei festem Achsabstand ist also ein solches †bersetzungsgetriebe mit straff gespannter Kette nicht mšglich.

Abb. 6: Kettenantrieb
Dass es in der Praxis trotzdem funktioniert (Abb. 6), mag folgende Grźnde haben: Die ZahnrŠder haben viel mehr ZŠhne und sind daher nŠher beim Kreis. Die AchsabstŠnde sind sehr klein und kšnnen durch den technischen Spielraum und die ElastizitŠt des Materials aufgefangen werden. Die Ketten sind nicht straff gespannt, schon wegen der Schwerkraft hŠngen sie etwas durch.
Website
Hans Walser: Aufwickeln (Vortrag)
http://www.walser-h-m.ch/hans/Vortraege/20190913-15/index.html