Hans Walser, [20160811]

Kettenlinie

Anregung: (BlŚsjš 2016)

1     Worum geht es?

Eine Kette gegebener LŠnge wird an zwei gleich hoch liegenden Punkten aufgehŠngt. Wie kšnnen die beiden AufhŠnge-Punkte verŠndert werden, ohne dass sich die Position des Scheitels (tiefster Punkt) der Kettenlinie verŠndert?

Die Abbildung 1 zeigt drei Positionsbeispiele.

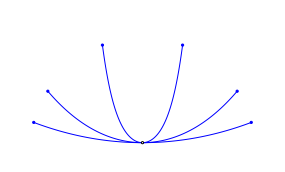
Abb. 1: Drei Kettenlinien gleicher LŠnge

2     Die Kettenlinie

Die Kettenlinie (Seilkurve, Kateonoide, engl: catenary) wird im Standardfall durch den Funktionsgrafen der Funktion

 

                                                                                                         (1)

 

beschrieben (Abb. 2). Diese Kettenlinie kann auch als Parameterkurve dargestellt werden:

 

                                                                                             (2)

 

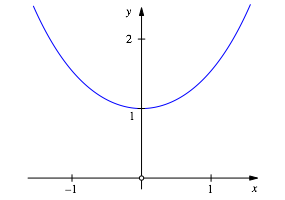
Abb. 2: y = cosh(x)

Die Bearbeitung der Kettenlinie geht auf Christiaan Huygens (1629-1695), Gottfried Wilhelm Leibniz (1646-1716) und Johann Bernoulli (1667-1748) zurźck.

Didaktisches: Die Kettenlinie ist von der quadratischen Parabel zu unterscheiden. Trotzdem wird in schulischen ArbeitsblŠttern die durchhŠngende Kette gelegentlich durch eine Parabel ămodelliertŇ. Das ist aber nur eine Modellierung des Šu§eren Scheins, keine Modellierung des physikalischen Hintergrundes.

3     BogenlŠnge der Kettenlinie

Die Kettenlinie ist eine der wenigen Kurven, deren BogenlŠnge sehr einfach zu berechnen ist. ZunŠchst ist:

 

                                                                                         (3)

 

Man beachte die gegenźber den Kreisfunktionen abweichenden Vorzeichen.

In der Parameterdarstellung lautet die Ableitung:

 

                                                                                               (4)

 

 

Fźr das Bogenelement ds erhalten wir:

 

                                                                   (5)

 

Fźr die BogenlŠnge s im Abschnitt  ergibt sich daraus:

 

                                                                   (6)

 

4     Symmetrische Kettenlinie durch den Ursprung

Fźr unsere Aufgabe setzen wir die konstante KettenlŠnge auf 2.

Die Kettenlinie zeichnen wir durch den Ursprung, das hei§t wir arbeiten mit der Darstellung:

 

                                                                                (7)

 

 

 

Auf die BogenlŠnge hat das keinen Einfluss, da der Zusatz  beim Ableiten wegfŠllt. Die AufhŠnge-Punkte sind symmetrisch zur y-Achse. Fźr  erhalten wir die BogenlŠnge:

 

                                                                             (8)

 

Diese LŠnge sollte nun 2 sein. Um dies zu erreichen, strecken wir die Kettenlinie vom Ursprung aus mit dem Faktor .

Wir erhalten so fźr jeden Parameterwert b > 0 eine Kettenlinie

 

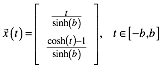                                                                                   (9)

 

 

mit der LŠnge 2, welche durch den Ursprung verlŠuft.

Fźr die Parameterwerte  ergeben sich die drei Beispiele der Abbildung 1.

5     AufhŠnge-Punkte

Fźr den Parameter b > 0 ergeben sich aus (9) fźr die AufhŠnge-Punkte der Kettenlinie die Koordinaten:

 

                                                             (10)

 

Somit kšnnen sich die linken beziehungsweise rechten AufhŠnge-Punkte auf folgenden Kurven bewegen (Abb. 3):

 

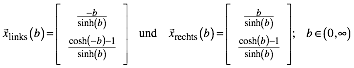                 (11)

 

 

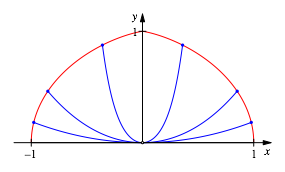
Abb. 3: Bahnkurven der AufhŠnge-Punkte

Der Autor wei§ nicht, wie diese Kurven hei§en. Die Abbildung 4 zeigt die Kurven als solche.

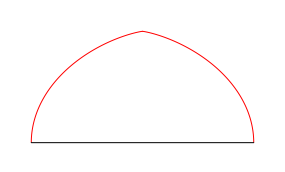
Abb. 4: Das Tor zur Kettenlinie

6     GrenzfŠlle

6.1    Gestreckter Fall

Fźr  streben die beiden AufhŠnge-Punkte gegen  beziehungsweise . Die Kettenlinie wird gestreckt, wenigsten theoretisch. Wegen der ElastizitŠt des Materials wird sie trotzdem ein bisschen durchhŠngen.

6.2    Schlaufe

Fźr  streben beide AufhŠnge-Punkte gegen . Wir erhalten eine Schlaufe mit Umkehrpunkt im Ursprung.

7     Bildergalerie

Die Fotos (Abb. 5) zeigen reale Beispiele mit Gro§mutters Goldkettchen.

Vorgehen: In Abbildung 4 Basislinie auf die LŠnge des Kettchens (49.8cm) skalieren. Niveaulinien zur horizontalen Orientierung einzeichnen. Der Drucker braucht drei DIN A4-Papiere. Diese auf Sto§ zusammenkleben und mit Magneten an die Kźhlschranktźre montieren. Bei zwei Magneten mit einer Zentralbohrung entsprechend dicke Drahtstifte einfźhren und dort das Kettchen aufhŠngen.

Abb. 5.1: Position 1

Abb. 5.2: Position 2

Abb. 5.3: Position 3

Abb. 5.4: Position 4

Abb. 5.5: Position 5

 

Literatur

BlŚsjš, Viktor (2016): How to Find the Logarithm of Any Number Using Nothing But a Piece of String. The College Mathematics Journal. Vol. 47, No. 2, March 2016, 95-100.