Hans Walser, [20200713]
Kettenwurzeln
1 Worum geht es?
Kettenwurzeln im trigonometrischen Kontext des Winkelhalbierens
2 Die Beispiele
2.1 Rechter Winkel
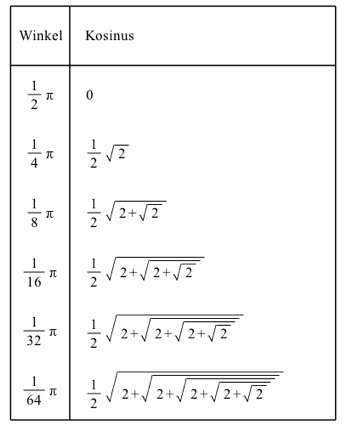
Tab. 1
2.2 60ˇ-Winkel
Tab. 2
2.3 72ˇ-Winkel
Tab. 3
Der 72ˇ-Winkel spielt in der Geometrie des regelmŠ§igen Fźnfecks und damit beim Goldenen Schnitt eine zentrale Rolle (Walser 2013a).
3 Hintergrund
Aus dem Additionstheorem
(1)
ergibt sich:
(2)
Daraus folgt durch Iteration:
(3)
und weiter
(4)
Wir sehen die Entwicklung der Kettenwurzel.
Die Tabelle 4 gibt die ersten Formeln.
Tab. 4: Fortlaufendes Winkelhalbieren
Wenn sich
nun 
durch eine
schšne Winkelformel oder durch eine rationale Zahl ausdrźcken lŠsst, ergibt
sich beim fortlaufenden Halbieren des Winkels eine Kettenwurzelformel.
4 Weitere Beispiele
4.1 Der kristallografische Winkel
Der Winkel
(5)
erscheint an verschiedenen Orten in der Kristallographie und der Geometrie. Er ist der Diederwinkel des regelmŠ§igen Tetraeders. Er ist auch der Schnittwinkel der beiden Diagonalen im DIN-Rechteck (Walser 2013b).
Die Tabelle 5 zeigt die zugehšrigen Kettenwurzeln.
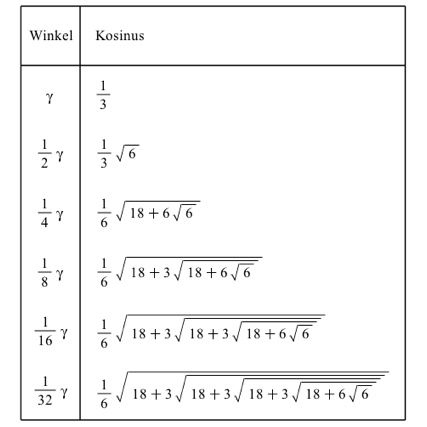
Tab. 5: Halbieren des kristallografischen Winkels
4.2 Im Lehrerdreieck
Im rechtwinkligen Dreieck mit dem SeitenverhŠltnis a:b:c = 3:4:5 (Abb. 1) ist:
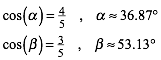(6)
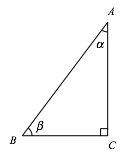
Abb. 1: Lehrerdreieck
Die Tabellen 6.1 und 6.2 zeigen die zugehšrigen Kettenwurzeln.
Natźrlich kann man bei allen pythagoreischen Dreiecken entsprechend vorgehen.
Tab. 6.1
Tab. 6.2
Literatur
Walser, H. (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Walser, H. (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.