Hans Walser, [20150124]

Kiepert-Hyperbel

1     Die Kiepert-Hyperbel

Der Kegelschnitt durch die drei Eckpunkte eines Dreieckes sowie dessen Schwerpunkt und Hšhenschnittpunt ist immer eine gleichseitige Hyperbel (Abb. 1), die so genannte Kiepert-Hyperbel (Eddy&Fritsch 1994), (Walser 2012).

 

Abb. 1: Kiepert-Hyperbel

 

Die Kiepert-Hyperbel hat viele schšne Eigenschaften.

In den folgenden Abbildungen sind der Schwerpunkt und der Hšhenschnittpunkt nicht mehr eingezeichnet, um die Figur leichter lesbar zu machen.

2     RegelmŠ§ige Vielecke

Wir setzen den drei Seiten des Dreiecks regelmŠ§ige Vielecke gleicher Eckenzahl an. Die Eckenzahl ist beliebig, in den folgenden Beispielen wurde mit FŸnfecken gearbeitet (Abb. 2).

 

Abb. 2: RegelmŠ§ige Vielecke

 

3     EinfŸgen von Dreiecken

Zwischen den Vielecken fŸgen wir gelbe Dreiecke ein gemŠ§ Abbildung 3.

 

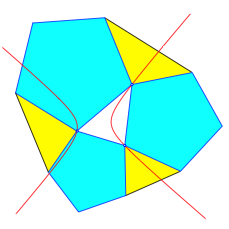
Abb. 3: Dreiecke einfŸgen

 

3.1    Schwerlinien

Nun zeichnen wir in die gelben Dreiecke jeweils die Schwerlinie, die auch durch die ecke des Ausgangsdreieckes geht (Abb. 4).

 

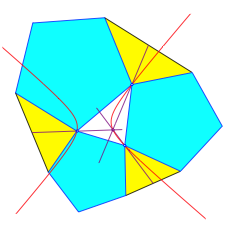
Abb. 4: Schwerlinien

 

Die TrŠgergeraden dieser drei Schwerlinien schneiden sich in einem Punkt, und dieser liegt auf der Kiepert-Hyperbel. Es handelt sich aber nicht um den Schwerpunkt des Ausgangsdreieckes.

3.2    Hšhen

Dasselbe Spielchen funktioniert auch mit Hšhen (Abb. 5).

 

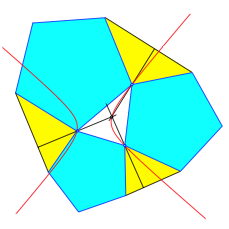
Abb. 5: Hšhen

 

4     Grš§ere gelbe Dreiecke

Die Dreiecke kšnnen auch durch Diagonalen der regelmŠ§igen Vielecke gebildet werden (Abb. 6). Es wurden regelmŠ§ige Neunecke angesetzt. Die gelben Dreiecke haben Diagonalen als Seiten, welche zwei Neuneckecken Ÿberspringen. In den gelben Dreiecken wurden die Schwerlinien verwendet.

 

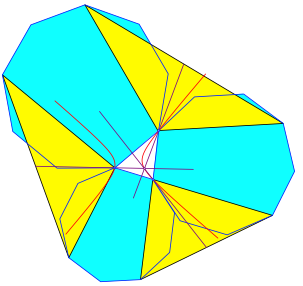
Abb. 6: Grš§ere gelbe Dreiecke

 

5     Allgemeiner Sachverhalt

Die Beispiele sind SonderfŠlle eines allgemeinen Sachverhaltes. Wir setzen dem Dreieck Šhnliche gleichschenklige Trapeze an gemŠ§ Abbildung 7. Dazwischen fŸgen wir gelbe Dreiecke ein.

 

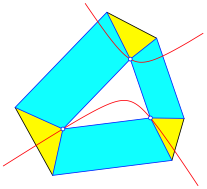
Abb. 7: €hnliche gleichschenklige Trapeze

 

Nun erhalten wir sowohl mit den Schwerlinien wie auch mit den Hšhen der gelben Dreiecke einen Schnittpunkt auf der Kiepert-Hyperbel (Abb. 8 und 9).

 

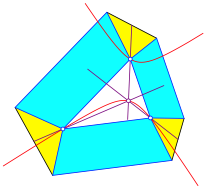
Abb. 8: Schwerlinien

 

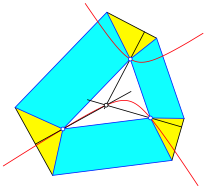
Abb. 9: Hšhen

 

Beweis fehlt, mit DGS ŸberprŸft.

6     Sonderfall im allgemeinen Fall

Nun ist es aber so, dass eine konsistente VerŠnderung der Trapezhšhen die gelben Au§endreiecke zwar Šhnlich verŠndert, aber an der Lage sowohl der relevanten Schwerlinien wie auch der relevanten Hšhen nichts Šndert. Wichtig sind lediglich die Trapezwinkel. Wir kšnnen uns daher auf GrenzfŠlle von gleichschenkligen Trapezen beschrŠnken, nŠmlich auf gleichschenklige Dreiecke. Die Abbildung 10 zeigt die Situation fŸr Schwerlinien in den gelben Dreiecken.

 

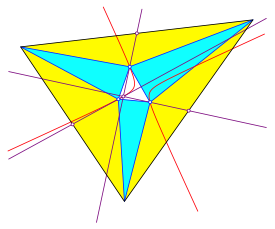
Abb. 10: Schwerlinien

 

Die Abbildung 11 zeigt die Situation fŸr Hšhen in den gelben Dreiecken.

 

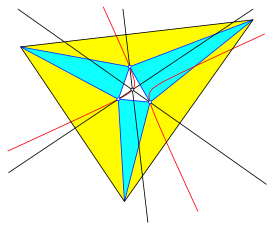
Abb. 11: Hšhen

 

Einfach zur Erinnerung: Mit den angesetzten gleichschenkligen Dreiecken kann auch ohne die gelben Dreiecke ein Punkt der Kiepert-Hyperbel bestimmt werden (Abb. 12). Dies ist die klassische Art, die Kiepert-Hyperbel zu generieren.

 

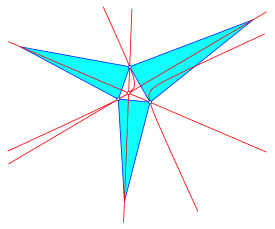
Abb. 12: Klassisch

 

Die Abbildung 13 zeigt die †berlagerung der oben diskutierten Mšglichkeiten.

 

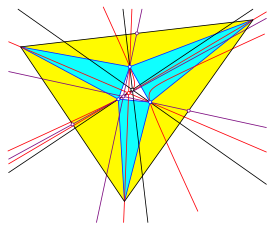
Abb.13: †berlagerung

 

Literatur

Eddy, R.H. / Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June, p. 188 - 205.

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0.