Hans Walser, [20200219]
Kiepert-Hyperbel
1 Worum geht es?
Alternative Methode zur Generierung der Kiepert-Hyperbel
Numerisch źberprźft. Keine Beweise
2 Die Kiepert-Hyperbel
Die Kiepert-Hyperbel ist der Kegelschnitt durch die drei Ecken eines Dreiecks, den Schwerpunkt und den Hšhenschnittpunkt. Sie ist gleichseitig. Sie enthŠlt etliche andere ăbesondere PunkteŇ im Dreieck, etwa den Fermat-Punkt.
3 Das Vorgehen
Einem beliebigen Dreieck setzen wir (Halb-)kreise an und tragen sechs gleiche Winkel ab gemŠ§ Abbildung 1.
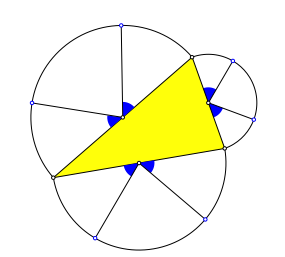
Abb. 1: Dreieck. Halbkreise. Winkel
Nun ergŠnzen wir zu Parallelogrammen (Abb. 2).
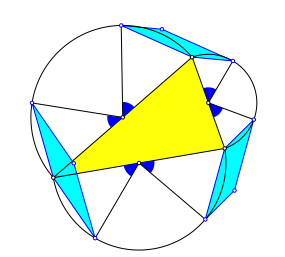
Abb. 2: Parallelogramme
Die TrŠgergeraden der drei von einer Dreiecksecke ausgehenden Parallelogramm-Diagonalen schneiden sich in einem Punkt (Abb. 3). Numerisch źberprźft.
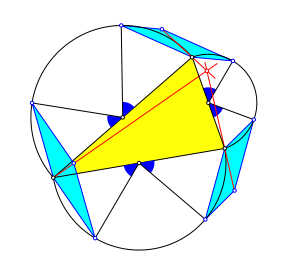
Abb. 3: Schnittpunkt
Der Schnittpunkt liegt auf der Kiepert-Hyperbel (Abb. 4).
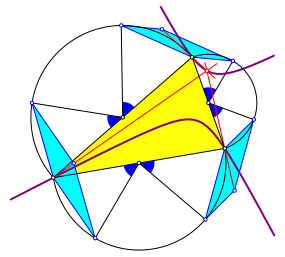
Abb. 4: Kiepert-Hyperbel
4 Parametrisierung
Wenn wir den blauen Winkel von 0ˇ bis 360ˇ variieren, ergibt sich die gesamte Kiepert-Hyperbel. Die Parallelogramme źberschneiden sich.
5 SonderfŠlle
Spezielle Werte fźr den blauen Winkel:
Fźr 60ˇ ergibt sich der Šu§ere Fermat-Punkt. Die drei Parallelogramm-Diagonalen sind gleich lang. Ihre TrŠgergeraden schneiden sich unter Winkeln von 60ˇ.
Fźr 180ˇ ergibt sich der Schwerpunkt. Die drei Parallelogramme sind flŠchengleich, aber nicht kongruent.
Fźr 300ˇ ergibt sich der innere Fermat-Punkt. Die drei Parallelogramm-Diagonalen sind gleich lang. Ihre TrŠgergeraden schneiden sich unter Winkeln von 60ˇ.
Fźr die Grenzwerte 0ˇ oder 360ˇ nŠhern sich die TrŠgeregeraden der Diagonalen den Dreieckshšhen an. Es ergibt sich der Hšhenschnittpunkt.
Literatur
Eddy, R.H. / Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June, p. 188 - 205.
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0.
Websites
Hans Walser: Kiepert-Hyperbel
http://www.walser-h-m.ch/hans/Miniaturen/K/Kiepert/Kiepert.htm