1 Worum geht es?

Die für die Kiepert-Hyperbel benötigte Konstruktion liefert weitere Schnittpunkte, die auf einem Kegelschnitt liegen.

2 Vorgehen

Einem beliebigen Dreieck setzen wir ähnliche gleichschenklige Dreiecke auf (Abb. 1).

Abb. 1: Ähnliche gleichschenklige Dreiecke

Wir verlängern die Schenkel und bringen sie zum Schnitt gemäß Abbildung 2.

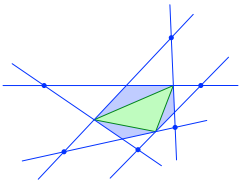
Abb. 2: Sechs Schnittpunkte

Die sechs Schnittpunkte liegen auf einem Kegelschnitt (Abb. 3).

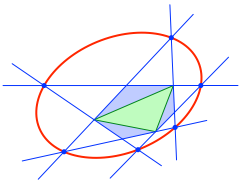
Abb. 3: Kegelschnitt

Die Abbildung 4 zeigt die zugehörige Animation.

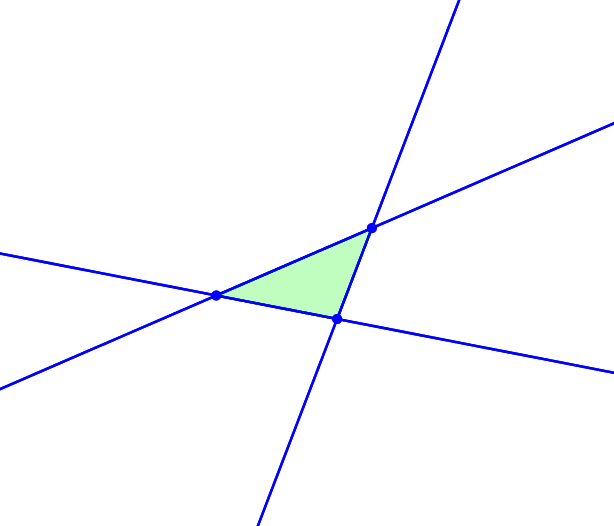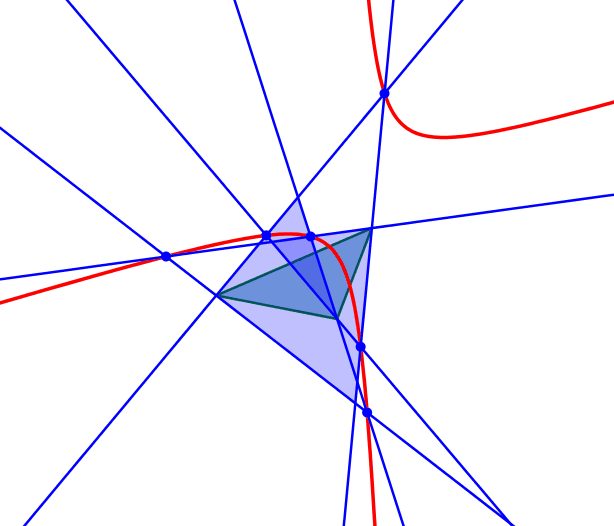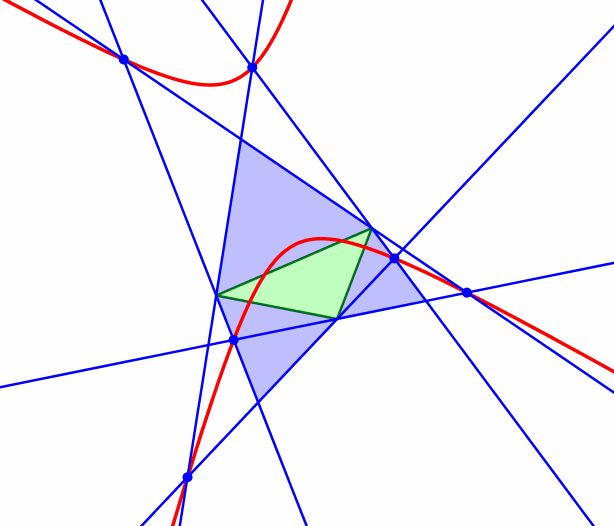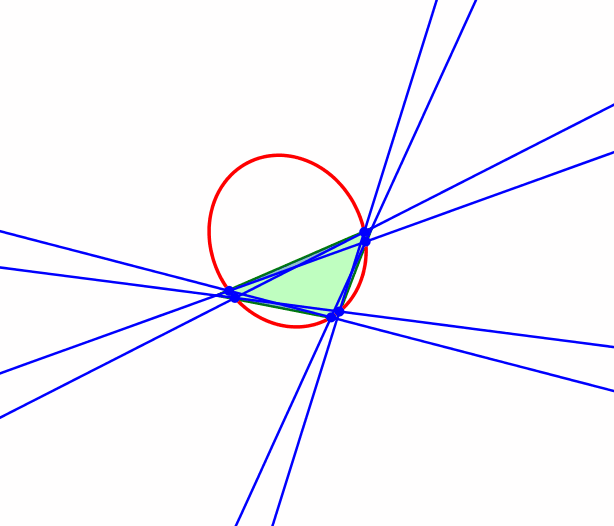
Abb. 4: Animation

Literatur

Eddy, R.H. / Fritsch, R. (1994): The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June, p. 188 - 205.

Walser, Hans (2006): 99 Points of Intersection. Examples – Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America. ISBN 0-88385-553-4

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Weblinks

Hans Walser: Kiepert-Hyperbel

http://www.walser-h-m.ch/hans/Miniaturen/K/Kiepert/Kiepert.htm

Hans Walser: Kiepert-Hyperbel

http://www.walser-h-m.ch/hans/Miniaturen/K/Kiepert2/Kiepert2.htm