Hans Walser, [2023067]

Kinematisches 18-Eck

1 Worum es geht

Abbiegen eines Polygonzuges im Dreiertakt.

2 Startfigur

Wir arbeiten mit einem Polygonzug mit 18 gleich langen Abschnitten. Wir beginnen in gestrecktem Zustand.

3 Abbiegen

Nun biegen wir bei jedem dritten Knoten im negativen Drehsinn, also um –t, bei den übrigen Knoten aber im positiven Drehsinn, also um +t. Die Abbildung 1 zeigt die Situation für t = π/12, also 15°.

Abb. 1: Abbiegen um 15°

4 Animation

In der Abbildung 2 wird t variiert.

Abb. 2: Variation von t

Wir erhalten schöne Zwischenfiguren.

5 Zwischenfiguren

Der Streckenzug schließt sich bei einer aus sieben regelmäßigen Sechsecken zusammengesetzten Figur (Abb. 3).

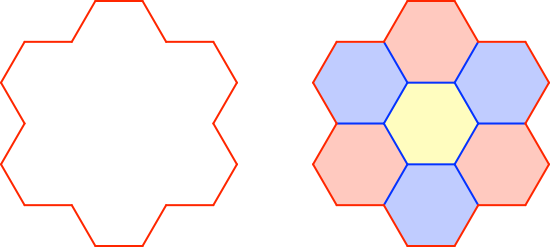
Abb. 3: Sechsecke

In die Situation mit drei überlappten Abschnitten lassen sich fünf Fünfecke einbauen (Abb. 4). In der Mitte erscheint ein Stern mit fünf Spitzen.

Abb. 4: Fünfecke

Bei sechs überlappten Abschnitten entsteht ein aus fünf Quadraten zusammengesetztes Kreuz (Abb. 5).

Abb. 5: Quadrate

Bei neun überlappten Abschnitten entsteht eine aus drei Dreiecken zusammengesetzte Figur (Abb. 6).

Abb. 6: Dreiecke

Die Abbildung 7 zeigt einen irritierenden Sonderfall. Für t = 4π/5, also 144°, ergibt sich ein Polygonzug mit scheinbar ungleich langen Abschnitten. Tatsächlich aber haben wir eine teilweise Überlappung von gleich langen Abschnitten. Dies kann durch die Nummerierung der Knoten sichtbar gemacht werden. In den rot markierten Knoten wurde um +144° abgebogen, in den blau markierten um –144°.

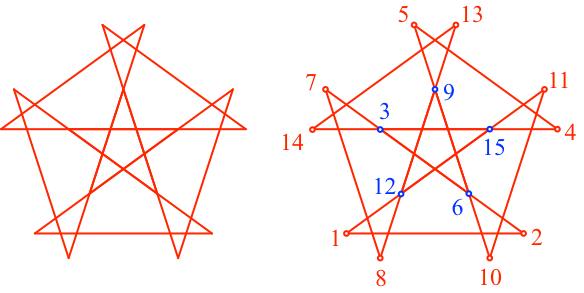
Abb. 7: Interessanter Sonderfall

Lediglich die letzten drei Abschnitte überlappen vollständig mit den ersten drei. Daher hört die Nummerierung schon bei 15 auf und nicht erst bei 18.

Bei 18 überlappten Abschnitten bleibt lediglich eine Strecke sichtbar. Wird der Imagination der Leserinnen und Leser überlassen.

Die Abbildung 8 zeigt einen Ausschnitt der Abbildung 2 mit den in den Abbildungen 3 bis 7 gezeigten Sonderfällen.

Abb. 8: Ausschnitt

6 Ausblick

Zurückdrehen in einem anderen Rhythmus, zum Beispiel bei jedem vierten Knoten.

Weblink

Hans Walser: Zick-Zack

http://www.walser-h-m.ch/hans/Miniaturen/Z/Zick-Zack/Zick-Zack.html