Hans Walser, [20121110]
Kirchendach Winkeln. RegelflŠchen
Anregung: R. L.
1 RegelflŠchen
In der Grundrissebene
eines rŠumlichen Koordinatensystems sei ein Rechteck mit den Begrenzungen 
und 
gegeben.
Weiter seien fŸr 
eine
Profilfunktion 
und fŸr 
eine Profilfunktion
gegeben.
Wir verbinden nun die
Punkte 
und 
geradlinig. Dadurch entsteht eine so
genannte RegelflŠche.
FŸr diese RegelflŠche gilt die Darstellung:
Die Funktion ist linear bezŸglich x. Dies ist eine Folge der geradlinigen Verbindung. BezŸglich y ergibt sich der Grad aus dem hšheren der beiden Grade von f beziehungsweise g.
2 Beispiele
2.1 SattelflŠche
Wir wŠhlen 
und 
. Weiter sei 
und 
. Die beiden Profilfunktionen sind also linear.
Wir erhalten fŸr die RegelflŠche:
Die Abbildung 1 zeigt diese RegelflŠche. Es handelt sich um ein so genanntes Paraboloid.
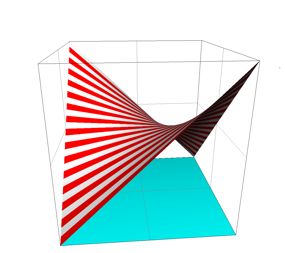
Abb. 1: Paraboloid
Die geradlinigen Verbindungen sind rot angegeben.
In diesem Beispiel ist auch die Konterlattung geradlinig (Abb. 2). Ein Paraboloid ist also in doppelter Hinsicht eine RegelflŠche.
Abb. 2: Konterlattung
2.2 Parabolische Profilfunktionen
Wir arbeiten mit den
quadratischen Profilfunktionen 
und 
. Wir erhalten die RegelflŠche der Abbildung 3.
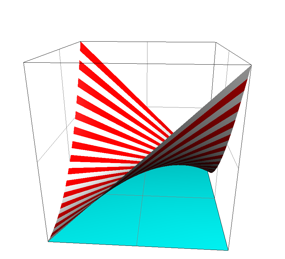
Abb. 3: Parabolische Profilfunktionen
Die Konterlattung ist jetzt nicht mehr gradlinig, sondern parabelfšrmig (Abb. 4).
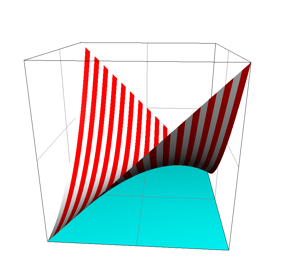
Abb. 4: Parabelfšrmige Konterlattung
3 Dach der Kirche Winkeln
Es ist [Angaben in m] 
und 
. Weiter arbeiten wir mit den beiden Profilfunktionen:
und
Diese Profilfunktionen sind vom vierten Grad. Die Koeffizienten der hohen Grade sind klein, um Ausrei§er zu vermeiden. Die Kurven wurden vermutlich experimentell erarbeitet. Die Abbildung 5 zeigt rot den Funktionsgrafen von f und blau den Funktionsgrafen von g.
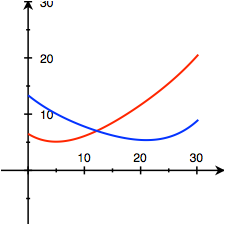
Abb. 5: Funktionsgrafen
Die Abbildung 6 zeigt die RegelflŠche mit den geraden Verbindungen.
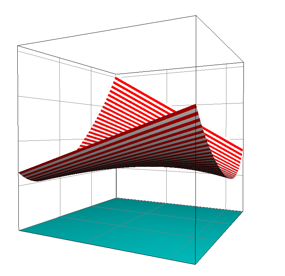
Abb. 6: RegelflŠche
Die Konterlattung ist gekrŸmmt (Abb. 7).
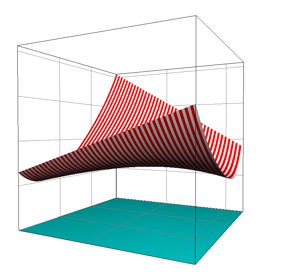
Abb. 7: Konterlattung
4 Weitere Beispiele von RegelflŠchen
4.1 Rotationshyperboloid
Wir ersetzen die Grafen der Profilfunktionen durch Kreise, die relativ zueinander etwas verdreht sind. Im Beispiel der Abbildung 8 sind sie um 90¡ verdreht.
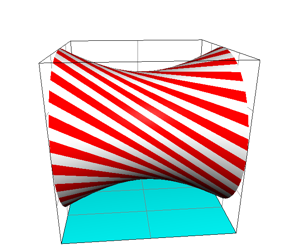
Abb. 8: Rotationshyperboloid
Rotationshyperboloide werden mit senkrechter Rotationsachse bei KŸhltŸrmen von Kraftwerken verwendet.
Ein Rotationshyperboloid enthŠlt aus SymmetriegrŸnden eine zweite Schar von Geraden, ist also wie das Paraboloid der Abbildungen 1 und 2 in doppelter Hinsicht eine RegelflŠche (Abb. 9).
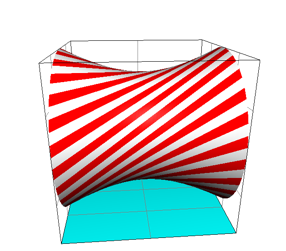
Abb. 9: Zweite Geradenschar
Die ãKonterlattungÒ besteht aus Kreisen (Abb. 10). Im Jargon der Geografen sind das so genannte Breitenkreise.
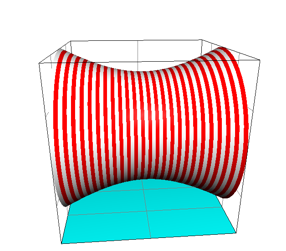
Abb. 10: Breitenkreise
4.2 WendelflŠche
Wir bewegen eine Strecke von links nach rechts und drehen sie gleichzeitig um die horizontale Mittelsenkrechte. Es entsteht eine SchraubenflŠche oder mit senkrechter Schraubachse eine WendelflŠche (Abb. 11). WendelflŠchen werden bei Parkhausauffahrten oder Kehrtunnels (Gotthardbahn) verwendet.
Abb. 11: SchraubenflŠche
Die ãKonterlattungÒ besteht aus Schraubenlinien (Spiralen, Abb. 12).
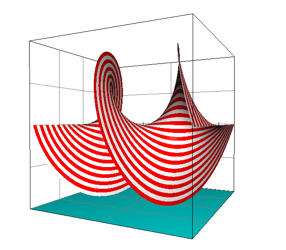
Abb. 12: Schraubenlinien
4.3 Mšbiusband
Die Abbildung 13 zeigt das klassische Mšbiusband.
Abb. 13: Mšbiusband
Die ãKonterlattungÒ besteht aus geschlossenen verschlungenen Kurven (Abb. 14).
Abb. 14: Wie viele geschlossene rote Kurven hat es?