Hans Walser, [20121223]

Kissing Numbers

Anregung: [Lagarias/Zong 2012]

1 Worum geht es?

Die Frage der Berührzahl (kissing number) wird am Kreis und speziellen gleichschenkligen Dreiecken besprochen.

2 Kreis und Ellipse

Ein Kreis kann von 6 dazu kongruenten Kreisen so eingerahmt werden, dass jeder der sechs Kreise den Ausgangskreis berührt (Abb. 1). Der Kreis hat die Kissing Number .

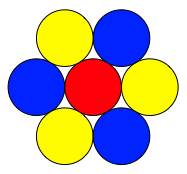
Abb. 1: Kreise

Nun können wir die Kreise auseinanderziehen und erhalten Ellipsen (Abb. 2).

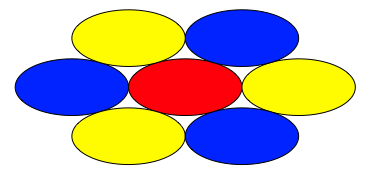
Abb. 2: Ellipsen

Allerdings bringen wir durch Verdrehen weitere Ellipsen an die Ausgangsellipse und haben erst noch etwas Spielraum (Abb. 3).

Abb. 3: Verdrehte Ellipsen

Wir sehen, dass „lang und schmal“ die Berührzahl erhöht.

3 Gleichschenklige Dreiecke

3.1 Gleichseitiges Dreieck

Das Gleichseitige Dreieck hat die Berührzahl (Abb. 4).

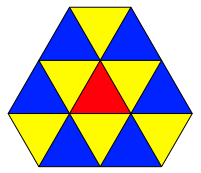
Abb. 4: Gleichseitiges Dreieck

Die Lösung lässt sich in ein regelmäßiges Dreiecksraster einbetten.

Das halbe gleichseitige Dreieck, also das Dreieck mit Winkeln 30°, 60° und 90°, hat die Berührzahl (Abb. 5).

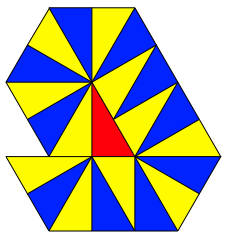
Abb. 5: Halbes gleichseitiges Dreieck

3.2 Gleichschenkliges Dreieck mit Spitzenwinkel 36°

Das so genannte Goldene Dreieck mit den Winkeln 36°, 72° und 72° (vgl. [Walser 2009]) hat die Berührzahl (Abb. 6).

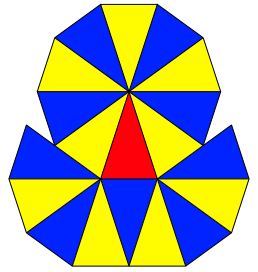
Abb. 6: Goldenes Dreieck

Die Figur lässt sich nicht in ein Raster aus goldenen Dreiecken einbetten.

Es gibt noch eine zweite Lösung (Abb. 7).

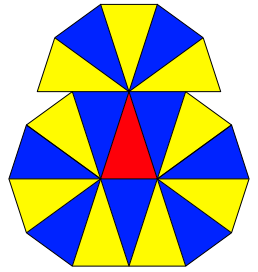
Abb. 7: Zweite Lösung

3.3 Spitzenwinkel 180°/7

Das gleichschenklige Dreieck mit dem Spitzenwinkel führt zu Figuren mit der Berührzahl (Abb. 8).

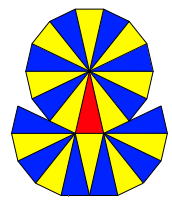
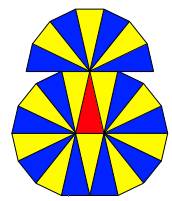
Abb. 8: Berührzahl 24

Die Beispiele der Abbildungen 4, 6, 7 und 8 fassen wir tabellarisch zusammen. In allen Fällen haben wir ein gleichschenkliges Dreieck mit einem Spitzenwinkel von . Es gilt dann:

	Gleichseitiges Dreieck	Goldenes Dreieck
Spitzenwinkel	60° = 180°/3	36° = 180° / 5	180°/7
n	2	3	4
Berührzahl k	12	18	24

Natürlich vermuten wir die arithmetische Folge .

Allerdings gibt es zu noch eine Lösung (Abb. 9), und diese Lösung hat sogar Spielraum. Der Spielraum reicht allerding nicht aus, um ein zusätzliches Dreieck einzufügen. Trotzdem mahnt das Beispiel zur Vorsicht.

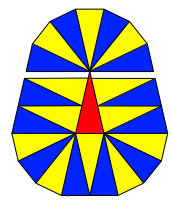
Abb. 9: Lösung mit Spielraum

3.4 Spitzenwinkel 20° = 180°/9

Es ist nun n = 5. Die Abbildung 10 zeigt die beiden bekannten Lösungen mit je k = 30. Das passt in die arithmetische Folge.

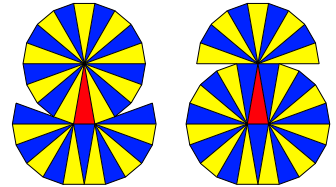
Abb. 10: Spitzenwinkel 20°

Die „Lückenlösung“ führt auch nach Verbesserung nur zu k = 29 (Abb. 11).

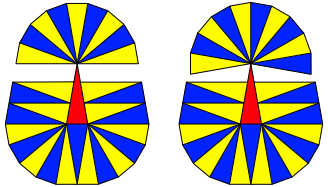
Abb. 11: Die Lückenlösung ist schlechter

3.5 Spitzenwinkel 180°/11

Nun ist n = 6. Die Abbildung 12 zeigt die beiden üblichen Lösungen. Es ist k = 36, gemäß der arithmetischen Folge.

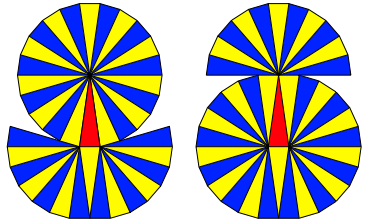
Abb. 12: Spitzenwinkel 180°/11

Die „Lückenlösung“ führt zunächst ebenfalls zu k = 36, durch Verdrehen des „Kopfes“ können wir aber k = 37 erreichen und sind damit besser als die arithmetische Folge (Abb. 13).

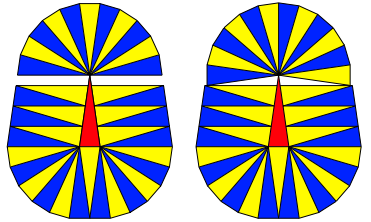
Abb. 13: Verbesserung der Lückenlösung

3.6 Spitzenwinkel 180°/13

Nun ist n = 7. Die Abbildung 14 zeigt die beiden üblichen Lösungen. Es ist k = 42, gemäß der arithmetischen Folge.

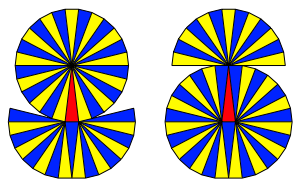
Abb. 14: Spitzenwinkel 180°/13

Die Lückenlösung führt ohne Kopfwackeln zu einer Lösung mit k = 44, also besser als die arithmetische Folge (Abb. 15). Und es hat immer noch etwas Spielraum.

Abb. 15: Die Lückenlösung ist besser

3.7 Tabellarische Übersicht

n	2*n-1	Arithmetische Folge	Lückenlösung	Wackellösung	Optimale Lösung
2	3	12	12	12	12
3	5	18	16	17	18
4	7	24	24	24	24
5	9	30	28	29	30
6	11	36	36	37	37
7	13	42	44	44	44
8	15	48	48	49	49
9	17	54	56	56	56
10	19	60	64	64	64
11	21	66	68	69	69
12	23	72	76	76	76
13	25	78	80	81	81
14	27	84	88	89	89
15	29	90	96	96	96
16	31	96	100	101	101
17	33	102	108	109	109
18	35	108	116	116	116
19	37	114	120	121	121
20	39	120	128	128	128
21	41	126	136	136	136
22	43	132	140	141	141
23	45	138	148	148	148
24	47	144	152	153	153
25	49	150	160	161	161
26	51	156	168	168	168
27	53	162	172	173	173
28	55	168	180	181	181
29	57	174	188	188	188
30	59	180	192	193	193

Literatur

[Lagarias/Zong 2012] Lagarias, Jeffrey C. and Zong, Chuanming: Mysteries in Packing Regular Tetrahedra. Notices oft he AMS, Volume 59, Number 11, Dezember 2012, p. 1540-1549.

[Walser 2009] Walser, Hans: Der Goldene Schnitt. 5., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig 2009. ISBN 978-3-937219-98-1