Hans Walser, [20200822]

Klammern

1 Worum geht es?

Endliche und unendliche Folgen mit Folgen als Folgenglieder.

2 Konstruktion

Wir beginnen mit einer Folge S₀, welche keine Folgenglieder enthält (leere Folge):

S₀ = [ ] (1)

Beide Klammern sind auf dem Grundlevel null. Wir haben die zugehörige Level-Folge:

0, 0 (2)

Die Abbildung 1.0 illustriert den Sachverhalt. Die öffnende Klammer ist durch ein rotes Quadrat, die schließende durch ein blaues dargestellt.

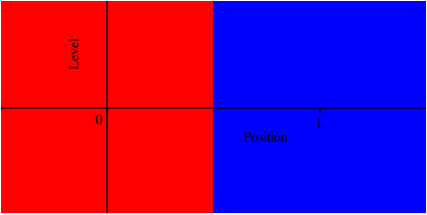
Abb. 1.0: Leere Folge

Weiter sei S₁ die Folge mit S₀ als einzigem Folgenglied:

S₁ = [S₀] = [[ ]] (3)

Die inneren Klammern sind auf dem Level 1. Wir haben also die Level-Folge:

0, 1, 1, 0 (4)

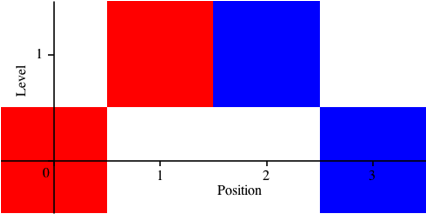
Abb. 1.1: Zwei Levels

Weiter sei S₂ die Folge mit den Folgengliedern S₀ und S₁:

S₂ = [S₀, S₁] = [[ ], [[ ]]] (5)

Die zugehörige Level-Folge der Klammern ist:

0, 1, 1, 1, 2, 2, 1, 0 (6)

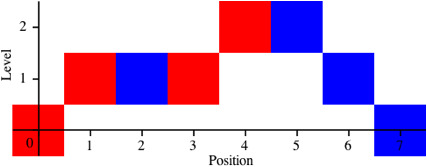
Abb. 1.2: Drei Levels

Weiter sei S₃ die Folge mit den Folgengliedern S₀, S₁ und S₂:

S₃ = [S₀, S_1, S₂] = [[ ], [[ ]], [[ ], [[ ]]]] (7)

Die zugehörige Level-Folge der Klammern ist:

0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 0 (8)

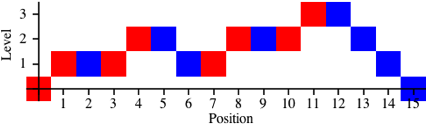
Abb. 1.3: Vier Levels

Übungshalber noch der nächste Schritt: Es sei S₄ die Folge mit den Folgengliedern S₀, S₁, S₂ und S₃:

S₄ = [S₀, S_1, S₂, S₃] = [[ ], [[ ]], [[ ], [[ ]]], [[ ], [[ ]], [[ ], [[ ]]]]] (9)

Zugehörige Level-Folge der Klammern:

0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 1, 0 (10)

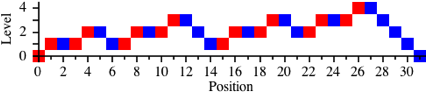
Abb. 1.4: Fünf Levels

Die Tabelle 1 gibt für die Figur der Abbildung 1.4 die Anzahlen der roten und der blauen Quadrate auf jedem Level an. Wir erkennend die Binomialkoeffizienten.

Level	Rote Quadrate	Blaue Quadrate
0	1	1
1	4	4
2	6	6
3	4	4
4	1	1

Tab. 1: Anzahlen der Quadrate pro Level

3 Rekursion

S₀ = [ ]

(11)

S_{n + 1} = [S₀, S₁, ... , S_n]

Für jedes S_n gibt es eine endliche Level-Folge b_n,k mit 2^{n + 1} Folgengliedern. Der Index k läuft von 0 bis 2^{n + 1} – 1. Die kleinsten Folgenglieder (b_n,0 am Anfang und am Schluss) haben den Wert 0. Es gibt zwei Folgenglieder ( und ) mit dem Höchstwert n.

So entsteht ein Zahlendreieck. In der Abbildung 2 ist es symmetrisch angeordnet, aber die Zahlwerte sind nicht symmetrisch.

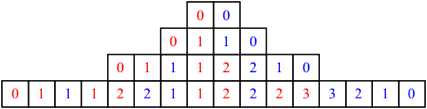
Abb. 2: Zahlendreieck

Das Zahlendreieck (die Matrix) b_n,k kann generiert werden wie folgt.

Zunächst setzen wir die Startwerte:

b[0,0] := 0 : (12)

b[0,1] := 0 :

Zur Farbgebung (im rgb-System) generieren wir eine zweite Matrix c_n,k mit den Startwerten:

c[0,0] := 0 : (13)

c[0,1] := 1 :

Die rekursive Berechnung (für n von 1 bis N) geht nun wie folgt:

for n from 1 to N do

for k from 0 to 2^n-2 do

b[n,k] := b[n-1,k]:

c[n,k] := c[n-1,k]:

end:

for k from 2^n-1 to 2*2^n-2 do (14)

b[n,k] := b[n-1,k-2^n+1]+1:

c[n,k] := c[n-1,k-2^n+1]:

end:

b[n, 2*2^n-1] := 0:

c[n, 2*2^n-1] := 1:

end:

Zum Element b_n,k gehört der Farbcode: rgb = [1 – c_n,k, 0, c_n,k].

4 Folge der Level-Folgen

Wir fassen die endlichen Level-Folgen (2), (4), (6), (8), (10), ... zu einer einzigen unendlichen Folge zusammen. Das sieht schrittweise aus wie folgt:

Für den Start n = 0 rhalten wir natürlich dasselbe wie (2):

0, 0 (15)

Die zugehörige Abbildung 3.0 entspricht der Abbildung 1.0.

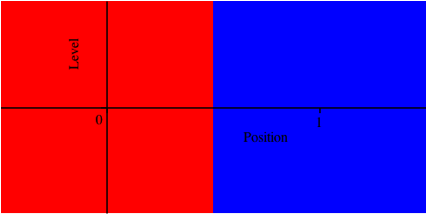
Abb. 3.0: Start

Für n = 1 ergibt sich:

0, 0, 0, 1, 1, 0 (16)

Die zugehörige Abbildung 3.1 ist eine Zusammensetzung der Abbildungen 1.0 und 1.1.

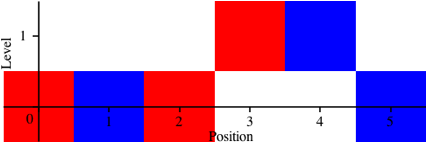
Abb. 3.1: Erster Schritt

Für n = 2 ergibt sich:

0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 2, 2, 1, 0 (17)

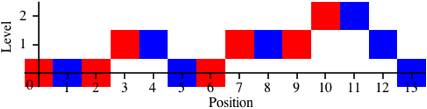
Abb. 3.2: Nächster Schritt

Für n = 3 erhalten wir:

0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 2, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 0 (18)

Abb. 3.3

Und noch für n = 4:

0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 2, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 0, 0, (19)

1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 1, 0

Abb. 3.4

Beim Schritt n haben wir 2(2^{n + 1} – 1) Folgenglieder.

Gesucht ist eine explizite oder rekursive Darstellung dieser Folge.

5 Rekursive Berechnung der Level-Folge

Zunächst berechnen wir nach (12), (13) und (14) die Elemente b_n,k und c_n,k.

Dann berechnen wir mit diesen Elementen:

for n from 0 to N do

for k from 0 to 2*2^n-1 do

a[2^(n+1)-2+k] := b[n,k]: (20)

d[2^(n+1)-2+k] := c[n,k]:

end:

end:

Die Folge a_m ist die gesuchte Level-Folge. Die Folge d_m dient der Kolorierung der Abbildungen.

Wenn uns nur die Folge a_m interessiert, können wir die Berechnung von c_n,k in (13) und (14) sowie die Berechnung von d_m in (20) weglassen.

Im Folgenden die Folgenglieder von a₀ bis a₁₀₂₁.

0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 2, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 4, 5, 5, 5, 6, 6, 5, 5, 6, 6, 6, 7, 7, 6, 5, 4, 3, 2, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 2, 2, 2, 3, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 4, 5, 5, 5, 6, 6, 5, 5, 6, 6, 6, 7, 7, 6, 5, 4, 3, 2, 1, 1, 2, 2, 2, 3, 3, 2, 2, 3, 3, 3, 4, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 4, 5, 5, 5, 6, 6, 5, 5, 6, 6, 6, 7, 7, 6, 5, 4, 3, 2, 2, 3, 3, 3, 4, 4, 3, 3, 4, 4, 4, 5, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 4, 5, 5, 5, 6, 6, 5, 5, 6, 6, 6, 7, 7, 6, 5, 4, 3, 3, 4, 4, 4, 5, 5, 4, 4, 5, 5, 5, 6, 6, 5, 4, 4, 5, 5, 5, 6, 6, 5, 5, 6, 6, 6, 7, 7, 6, 5, 4, 4, 5, 5, 5, 6, 6, 5, 5, 6, 6, 6, 7, 7, 6, 5, 5, 6, 6, 6, 7, 7, 6, 6, 7, 7, 7, 8, 8, 7, 6, 5, 4, 3, 2, 1, 0

Websites

Hans Walser: Klammern

http://www.walser-h-m.ch/hans/Miniaturen/K/Klammern/Klammern.htm