Hans Walser, [20190325]

Klebelaschen

1 Worum geht es?

Ein Minimalproblem

2 Problemstellung

Die Abbildung 1 zeigt die elf Würfelabwicklungen.

Abb. 1: Die elf Würfelabwicklungen

Jede Abwicklung hat 14 Außenkanten, die durch Aufschneiden des Würfelmodells an sieben Kanten entstanden sind. Für eine Vollverklebung des aufgewickelten Würfelmodells braucht es also sieben Klebelaschen. — Die sicherste Methode um das Zusammentreffen zweier Klebelaschen zu vermeiden besteht darin, an jeder zweiten Außenkante eine Klebelasche vorzusehen (Reißverschlussverfahren).

Und nun die Frage: Welches ist die Minimalzahl der Klebelaschen zur statischen Stabilisierung des Modells?

3 Bearbeitung

Das Experiment an realen Abwicklungen zeigt:

· Neun der elf Abwicklungen benötigen zwei Klebelaschen. In der Abbildung 2 sind das die ersten neun Abwicklungen. Die Lösungen sind exemplarisch, es gibt noch andere. Kanten, die mit einer Klebelasche verbunden werden müssen, sind in gleicher Farbe angegeben. Bei zwei roten Kanten muss also an einer der beiden roten Kanten eine Klebelasche angebracht werden, die dann mit der anderen roten Kante verklebt werden kann. Analog für zwei blaue Kanten.

· Die beiden letzten Abwicklungen kommen mit einer einzigen Klebelasche aus.

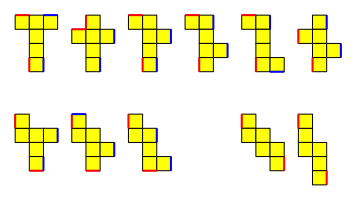
Abb. 2: Lösung

Die beiden letzten Abwicklungen lassen sich zu einem (unendlich langen) Bandornament fortsetzen (Abb. 3).

Abb. 3: Bandornamente

Ein solches Bandornament lässt sich (unendlich dünnes Material vorausgesetzt) (unendlich oft) auf einen gegebenen Würfel aufwickeln, ohne dass abstehende Ohren entstehen.

Literatur

Walser, Hans (2018): Der Würfel. Ansichten – Dimensionen – Modelle. Edition am Gutenbergplatz, Leipzig 2018. ISBN 978-3-95922-102-3.

Weblinks

Hans Walser: Klebelaschen

http://www.walser-h-m.ch/hans/Miniaturen/K/Klebelaschen/Klebelaschen.htm