Hans Walser, [20071003a]

Die Klothoide

Es wird ein Programm (MuPAD) vorgestellt, mit welchem jede durch die so genannte natürliche Gleichung gegebene Kurve approximativ gezeichnet werden kann. Insbesondere kann damit auch die Klothoide gezeichnet werden.

1 Kurvenkrümmung

Unter der Krümmung verstehen wir die momentane Richtungsänderung der Kurve beim Parameterwert s. Dabei soll s die Kurvenlänge sein (so genannter natürlicher Parameter). Das Integral

gibt die gesamte Richtungsänderung beim Durchlauf des Intervalls . Der Kehrwert von ist der lokale Krümmungskreisradius.

2 Die natürliche Gleichung einer Kurve

Die Gleichung legt eine Kurve im Wesentlichen, das heißt bis auf Anfangspunkt und Anfangsrichtung fest. Diese Gleichung heißt deshalb die natürliche Gleichung der Kurve.

Wir arbeiten in der komplexen Zahlenebene und bezeichnen den Anfangspunkt mit a und die Anfangsrichtung mit ,

3 Diskretisation durch eine Punktfolge

Wir wählen eine Schrittlänge und definieren eine Folge komplexer Zahlen mit den Startwerten und rekursiv:

Wir verbinden die Punkte dieser folge mit einem Polygonzug; das gibt eine Approximation der gesuchten Kurve.

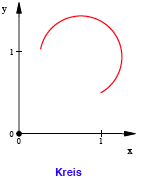
Beispiel: Die konstante Krümmung gibt einen Kreis mit dem Radius .

Laenge:=2:

p:=1+1/2*I:

phi:=PI/6:

deltas:=0.01:

kappa:=s->2:

n:=ceil(Laenge/deltas):

z[0]:=p:

z[1]:=z[0]+deltas*exp(I*phi):

for j from 1 to n-1 do

z[j+1]:=z[j]+(z[j]-z[j-1])*exp(I*deltas*kappa(j*deltas));

end_for:

Polygon:=i->plot::Polygon2d([[Re(z[i]), Im(z[i])], [Re(z[i+1]), Im(z[i+1])]], LineWidth=0.5,
LineColor=[1,0,0]):

Ursprung:=plot::Point2d([0,0], PointSize=2,
PointColor=[0,0,0]):

plot(Ursprung, Polygon(i)$i=0..n-1, Scaling=Constrained, TicksDistance=1, TicksBetween=0, Width=60, Height=60);

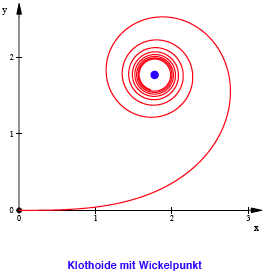
4 Die Klothoide

Die Klothoide, auch Spinnkurve oder Cornusche Spirale genannt, ist eine Kurve, deren Krümmung proportional zur Bogenlänge ist.

Die Klothoide hat also eine natürliche Gleichung von der Form . Die Schreibweise des Proportionalitätsfaktors hat historische Gründe. Die Klothoide wird im Bahn- und Straßenbau verwendet. Bei konstanter Durchfahrgeschwindigkeit, also bei ist dann die Radialbeschleunigung proportional zur Bogenlänge und damit zur Fahrzeit. Die Berechnung der Klothoide führt allerdings auf Integrale, die nicht elementar auswertbar sind. Man kann zeigen, dass der „Wickelpunkt“ A die Koordinaten hat.