1 Worum geht es

Potenzfunktionen und Wurzelfunktionen als Krümmungsfunktion

2 Potenzfunktionen als Krümmungsfunktion

Die Abbildung 1.1 zeigt die Standard-Klothoide.

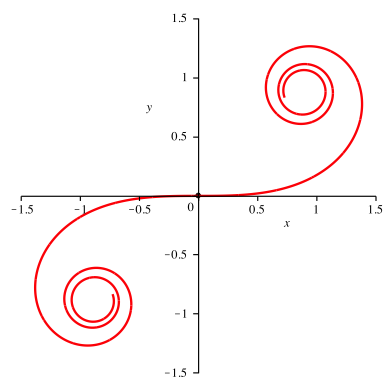
Abb. 1.1: Standard-Klothoide

Mit der Bogenlänge s gemessen vom Ursprung aus hat sie die lineare Krümmungsfunktion:

(1)

Wir verallgemeinern nun die Krümmungsfunktion zu einer Potenzfunktion vom Grad n:

(2)

Für n = 2 ergibt sich die Kurve der Abbildung 1.2. Die Krümmung ist größer oder gleich null.

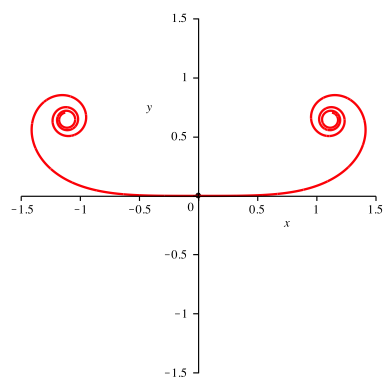
Abb. 1.2: Quadratische Krümmungsfunktion

Für n = 3 ergibt sich die Kurve der Abbildung 1.3. Im linken Teil haben wir eine negative Krümmung.

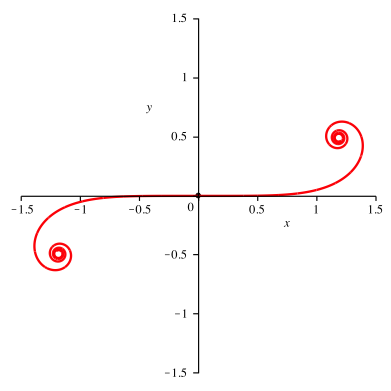
Abb. 1.3: Kubische Krümmungsfunktion

Für n = 4 ergibt sich die Kurve der Abbildung 1.4.

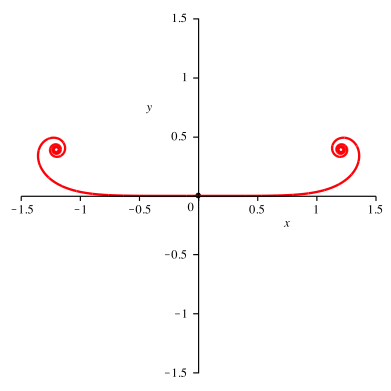
Abb. 1.4: Krümmungsfunktion vierten Grades

Der Wickelpunkt im ersten Quadranten nähert sich mit wachsendem n dem Einheitspunkt auf der x-Achse.

Die Abbildung 2 zeigt die Überlagerung der Kurven für n = 1, ... , 10.

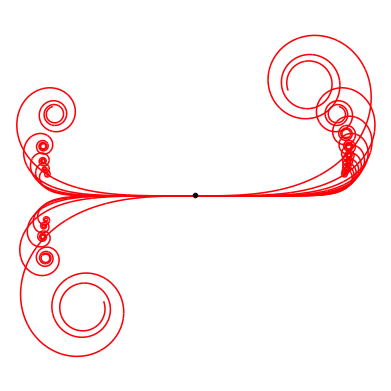
Abb. 2: Überlagerung

Für n = 0 (konstante Krümmung 1) ergibt sich der Einheitskreis (Abb. 3).

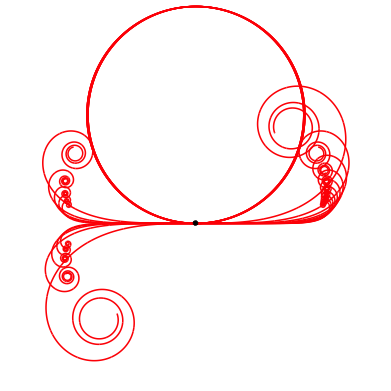
Abb. 3: Mit Einheitskreis

Der Einheitskreis wird mehrfach durchlaufen, wegen der iterativen numerischen Berechnung wird er unscharf dargestellt.

Die Animation 1 illustriert den Sachverhalt.

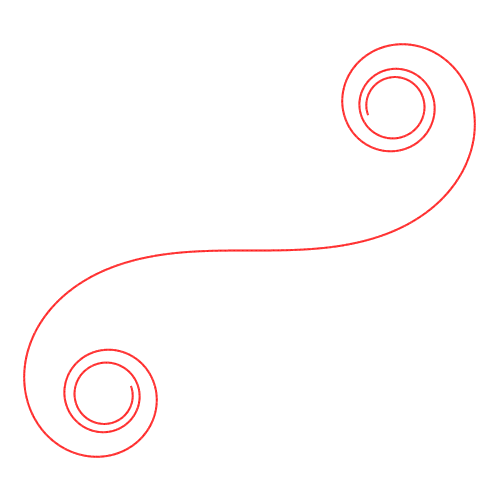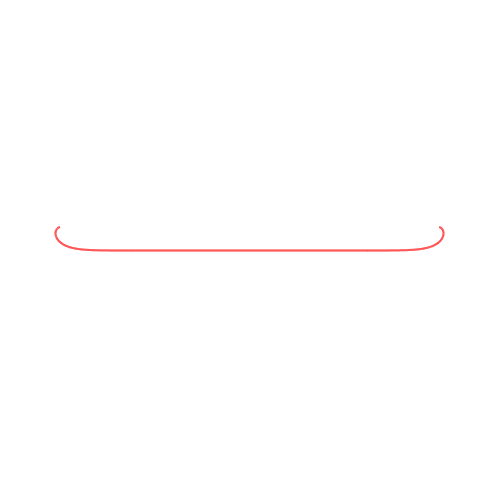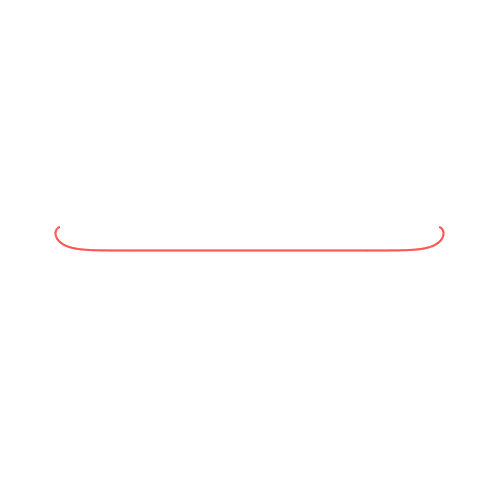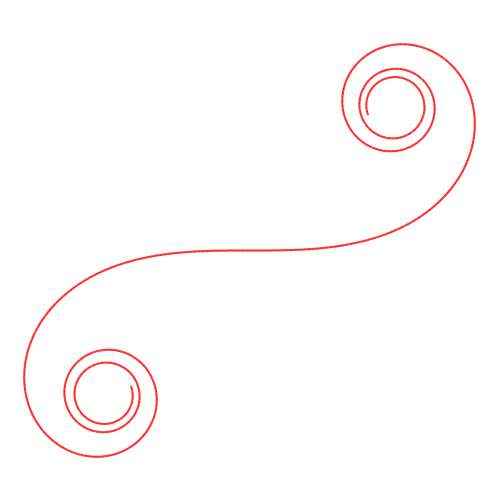
Animation 1: Potenzfunktionen als Krümmungsfunktion

Wir arbeiten mit der Krümmungsfunktion:

(3)

Dabei müssen wir uns auf den rechten Ast beschränken, um komplexe Werte zu vermeiden.

Die Abbildung 4 zeigt die Kurvenschar für .

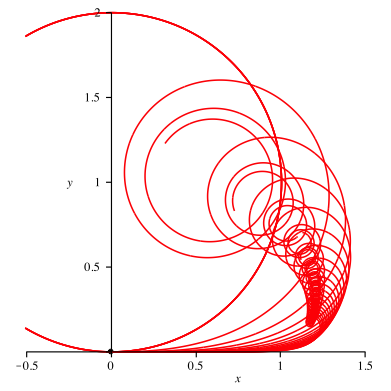
Abb. 4: Halbzahlige Exponenten

Die Animation 2 illustriert den Sachverhalt.

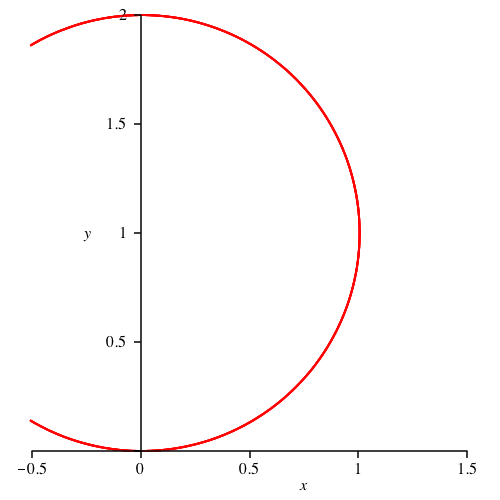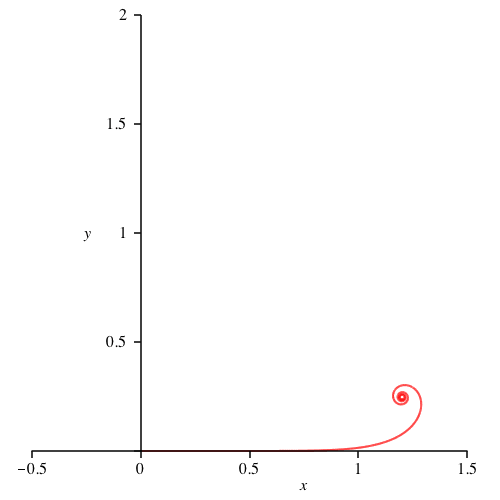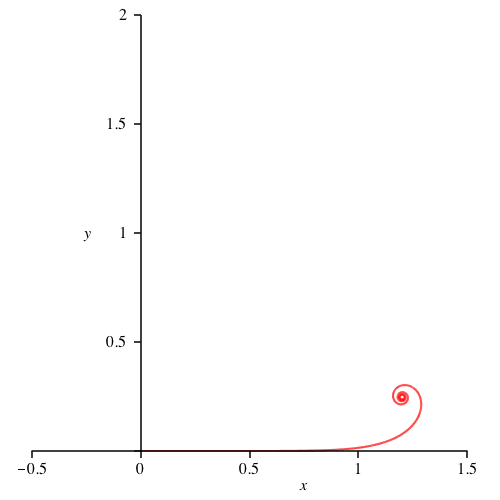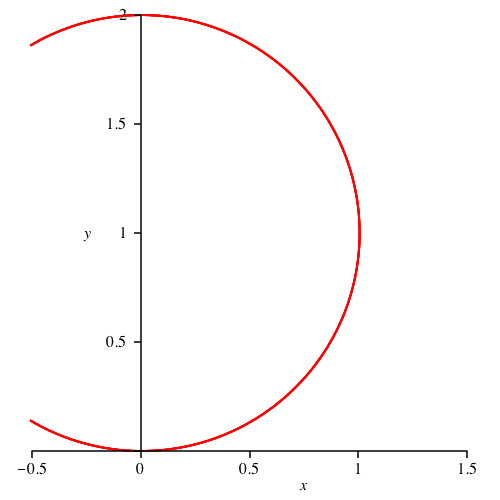
Animation 2: Gebrochene Exponenten (Viertel)

Websites

Hans Walser: Die Klothoide