Hans Walser, [20180415]
Knacknuss ohne Nussknacker
1 About
Spiel mit der vierten Dimension.
2 Das Problem
Die Abbildung 1 zeigt drei Nźsse in je zwei Ansichten.

Abb. 1: Drei Nźsse
Die Nuss a) ist eine normale Nuss mit zweiteiliger Symmetrie. Die Nuss b) hat eine dreiteilige Symmetrie, die Nuss c) gar eine vierteilige Symmetrie.
Die Frage ist, ob die Kerne ebenfalls die entsprechenden Symmetrien aufweisen. Um dies festzustellen, mźsste man die Nźsse knacken. Dadurch wird aber die Nussschale zerstšrt.
Wie erhalten wir den Nusskern, ohne die Nuss zu knacken?
3 In der Ebene
Die Abbildung 2 illustriert das zweidimensionale Analogon. Die Nussschale ist durch einen Kreisring modelliert:
![]() (1)
(1)
Der Kern ist durch eine Kreisscheibe modelliert:
![]() (2)
(2)

Abb. 2: In der Ebene
Es ist nicht mšglich, in der Ebene den Kern herauszuholen, ohne die Schale aufzubrechen.
4 Einbettung in den Raum
Hingegen kšnnen wir dies im Raum bewerkstelligen. Dazu mźssen wir allerdings die Situation in den Raum einbetten:
Aus (1) wird fźr die Nussschale:
![]() (3)
(3)
Aus (2) wird fźr den Kern:
![]() (4)
(4)
Die z-Achse wird beschrieben durch:
![]() (5)
(5)
Die Bedingungen (3) und (5) schlie§en sich aus. Die Bedingungen (4) und (5) haben den Ursprung als gemeinsamen Punkt. Wir kšnnen also im Raum (ăvon oben herŇ) in die Nussschale hineingreifen und den Kern herausnehmen, ohne die Nussschale zu berźhren oder gar zu zerstšren (Abb. 3).
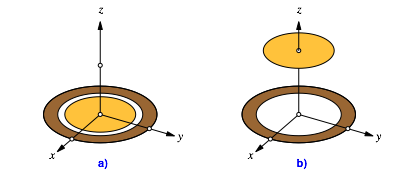
Abb. 3: Einbettung in den Raum
5 †berlegung im 4d-Raum
Wir źbertragen dieses Vorgehen in den vierdimensionalen Hyperraum.
Die Nussschale modellieren wir als 3d-Kugelschale:
![]() (6)
(6)
Den Kern modellieren wir als 3d-Kugel:
![]() (7)
(7)
Die w-Achse wird beschrieben durch:
![]() (8)
(8)
Wir kšnnen also entlang der w-Achse in die Nussschale hineingreifen und den Kern herausholen, ohne die Nussschale zu berźhren oder gar zu zerstšren.
So einfach ist das.