Hans Walser, [20160419]
The Knauth-Figure and Pythagoras
Motivation and idea: Eugen Jost, Thun, Switzerland
1 About
The Knauth Figure (fig. 1) in the context of the theorem of Pythagoras.
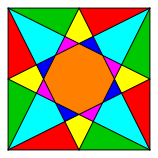
Fig. 1: The Knauth Figure
We will find differences between global symmetry and local symmetry.
2 The theorem of Pythagoras
We try to find a dissection proof of the theorem of Pythagoras in the special case of figure 2.
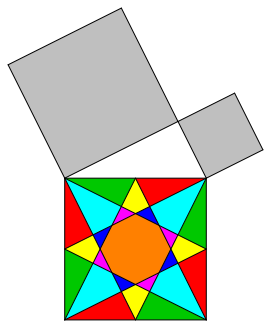
Fig. 2: Theorem of Pythagoras
3 Knauth tessellation
We extend the Knauth figure to a tessellation (fig. 3), where we cut out the three squares of the theorem of Pythagoras.

Fig. 3: Tessellation
This gives a dissection of the figure of Pythagoras (fig. 4). We still see the pattern of the global tessellation in the figure.
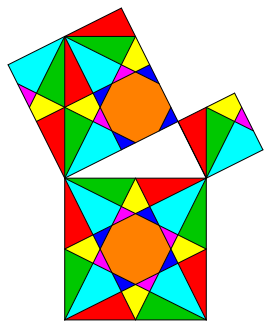
Fig. 4: Dissection
In this dissection we have a global symmetry due to the tessellation of figure 3. Every part fits in to the global pattern of figure 3.
But the dissections of the two small squares have no symmetry at all.
And there is another problem. We cannot move every individual part from the large square into the two small squares by translations only. We have to use some rotations about 90ˇ (clockwise). Figure 5 gives a dissection where this problem is fixed. But now the parts on the smallest square do no more fit in the global pattern of figure 3.
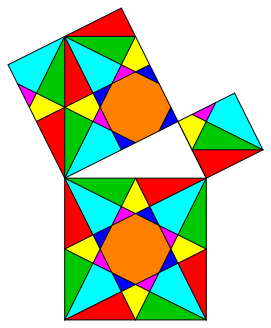
Fig. 5: Translation symmetry
Again the dissections in the two small squares have no symmetry.
4 Local symmetry
The dissection of figure 6 has symmetries in all the squares. But now the dissections in the small squares do not at all fit in the global pattern. We have only local symmetries in every square.
Every individual part of the largest square can be moved by translation only in the corresponding situation in one of the two smaller squares.
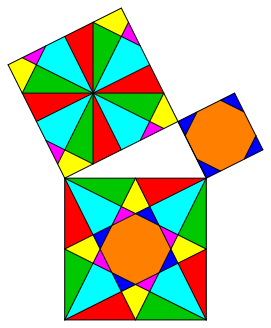
Fig. 6: Local symmetries
There are other solutions with the same properties like the solution of figure 6 (fig. 7, 8, and 9).
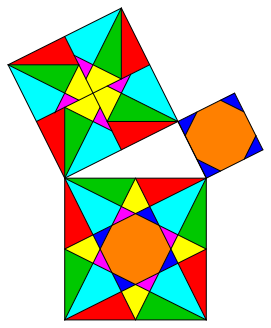
Fig. 7: Variation
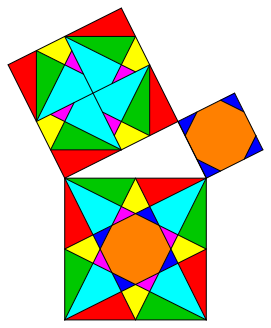
Fig. 8: Variation
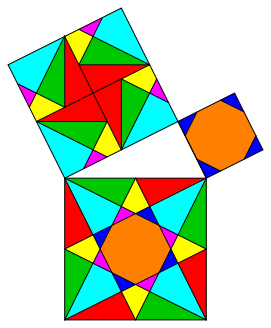
Fig. 9: Variation
The examples of figures 10 and 11 have less symmetry, but still local symmetry.
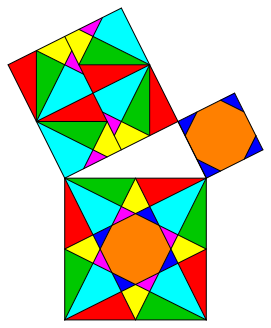 xs
xs
Fig. 10: Reduced local symmetry
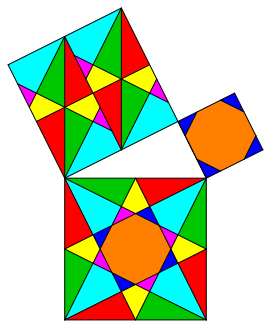
Fig. 11: Reduced symmetry