Hans Walser, [20100702a]
Sechs Punkte auf einer Hyperbel
1 Worum geht es?
Fźnf Punkte legen eine
Hyperbel fest. Sechs Punkte in allgemeiner Lage liegen daher nicht auf einer
Hyperbel. Es werden zwei Beispiele vorgestellt, in denen sechs Punkte auf einer
Hyperbel liegen.
2
Permutation von Koordinaten
Wir beginnen mit einem
beliebigen Dreieck in einem kartesischen Koordinatensystem. Dann halten wir die
x-Koordinaten fest und permutieren die
drei y-Koordinaten. Somit haben
wir sechs Dreiecke.
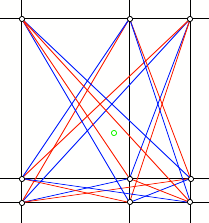
Sechs Dreiecke
Blau bedeutet, dass es
sich, ausgehend vom Startdreieck, um eine gerade Permutation handelt, rot
bedeutet die ungeraden Permutationen. Die sechs Dreiecke haben einen
gemeinsamen Schwerpunkt (grźn).
3
Umkreismittelpunkte
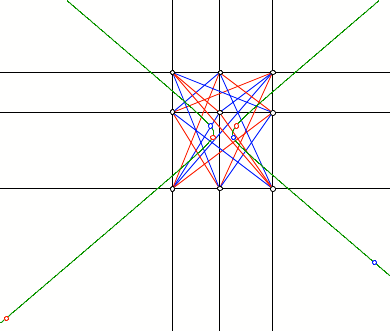
Umkreismittelpunkte auf
Hyperbel
Die sechs
Umkreismittelpunkte der Dreiecke liegen auf einer Hyperbel. Die Achsen der
Hyperbel sind parallel zu den Koordinatenachsen. Verifikation mit DGS.
4
Hšhenschnittpunkte
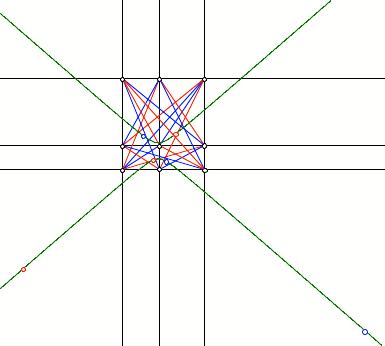
Hšhenschnittpunkte auf
Hyperbel
Die sechs
Hšhenschnittpunkte der Dreiecke liegen ebenfalls auf einer Hyperbel. Die Achsen
der Hyperbel sind parallel zu den Koordinatenachsen. Verifikation mit DGS.