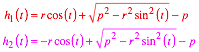Hans Walser, [20070302a]
Kolbenhub
Anregung: J. V., L. und [Vogel 2007]
Es wir der Kolbenhub als Funktion einer gleichm§igen Drehung der Kurbelwelle studiert.
1 Kurbelkreiszentrum auf Kolbenachse
Das ist der klassische Fall. Die Amplituden des Kolbenhubes entsprechen dem Kurbelkreisradius.
Bezeichnungen: Kurbelkreisradius r. Pleuelstangenlnge p.
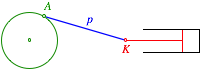
Klassischer Fall
Fr den Punkt A arbeiten wir mit den Bewegungsgleichungen:
![]()
Dann ergeben sich fr den Punkt K die Bewegungsgleichungen:
![]()
Die gesuchte Kolbenhubfunktion ist also:
![]()
Durch
Subtraktion von p erhalten wir eine
Funktion mit den Amplituden ![]() .
.
![]()
Das
Diagramm zeigt die Situation fr ![]() und
und ![]() .
.
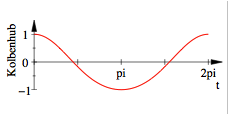
Kolbenhub
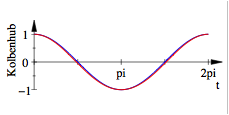
Dies sieht aus wie eine Kosinus-Kurve, ist aber keine (Nullstellen am falschen Ort), wie auch der Vergleich mit der echten Kosinus-Kurve (blau) in der folgenden Figur zeigt.
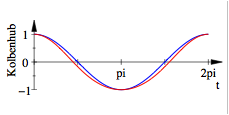
Vergleich mit Kosinus
Die
Abweichung ist bedingt durch die variierende Schrgstellung der Pleuelstange.
Bei kleiner Variation der Schrgstellung, also fr ![]() , ist die Abweichung gering. Im folgenden Beispiel ist
, ist die Abweichung gering. Im folgenden Beispiel ist ![]() und
und ![]() .
.
![]() und
und ![]() .
.
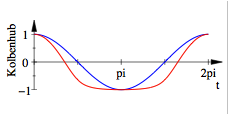
Spannender
ist es fr ![]() . Fr
. Fr ![]() und
und ![]() erhalten wir die
folgende Figur; das Schwungrad ist ziemlich gefordert, um den Kolben zur Umkehr
zu bewegen.
erhalten wir die
folgende Figur; das Schwungrad ist ziemlich gefordert, um den Kolben zur Umkehr
zu bewegen.
![]() und
und ![]()
Fr ![]() und
und ![]() erhalten wir ein
totes Intervall
erhalten wir ein
totes Intervall ![]() ; in dieser Situation schafft das Schwungrad den Turnaround
nicht mehr.
; in dieser Situation schafft das Schwungrad den Turnaround
nicht mehr.
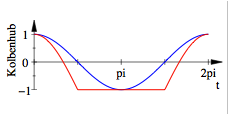
Totes Intervall
Fr ![]() funktioniert es
mechanisch nicht mehr.
funktioniert es
mechanisch nicht mehr.
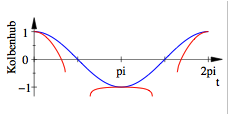
![]() und
und ![]()
2 Desaxierung
Es sei nun das Kurbelkreiszentrum gegenber der Kolbenachse um d desaxiert.
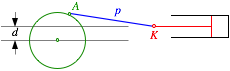
Desaxierung
d
Fr den Punkt A arbeiten wir wieder mit den Bewegungsgleichungen:
![]()
Nun ergeben sich fr den Punkt K die Bewegungsgleichungen:
![]()
Somit ergibt sich die Kolbenhubfunktion:
![]()
Fr ![]() ,
, ![]() und
und ![]() ergibt sich:
ergibt sich:
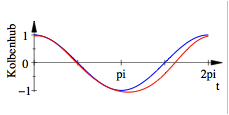
![]() ,
, ![]() und
und ![]()
Wir erhalten gegenber der blauen Kosinuskurve wieder eine Verzerrung.
Im
Beispiel ![]() ,
, ![]() und
und ![]() ergibt sich ein
totaler Hub, der offensichtlich gr§er als 2r
ist:
ergibt sich ein
totaler Hub, der offensichtlich gr§er als 2r
ist:
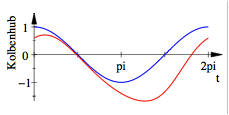
Hub gr§er als 2r
Einen
dramatischen toten Punkt erhalten wir fr ![]() ,
, ![]() und
und ![]() :
:
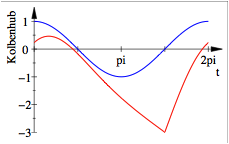
Toter
Punkt bei ![]()
3 180¡-V-Motor
3.1 Ohne Desaxierung
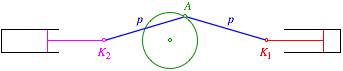
180¡-V-Motor
Fr den Punkt A arbeiten wir wieder mit den Bewegungsgleichungen:
![]()
Fr den
Punkt ![]() die
Bewegungsgleichungen
die
Bewegungsgleichungen
![]()
und fr
den Punkt ![]() :
:
![]()
Entsprechend
ergeben sich die Kolbenhubfunktionen (Vorzeichen bei ![]() beachten):
beachten):
Das
Diagramm zeigt die Situation fr ![]() und
und ![]() . Die Kurve fr
. Die Kurve fr ![]() ist rot, die
Kurve fr
ist rot, die
Kurve fr ![]() ist magenta
gezeichnet. Aus Symmetriegrnden haben wir einen Phasenversatz von
ist magenta
gezeichnet. Aus Symmetriegrnden haben wir einen Phasenversatz von ![]() .
.
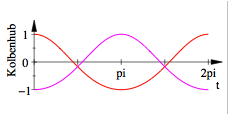
Kolbenhub
3.2 Mit Desaxierung
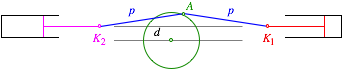
Desaxierung
Das ist im Prinzip die Situation in einem Rhombentriebwerk mit zwei Kolben. Der Rhombus ergibt sich durch Spiegelung an der Kolbenachse (vgl. [Vogel 2007], S. 15). Die Desaxierung d ist in der folgenden schematischen Zeichnung eingetragen.
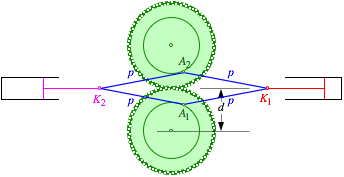
Rhombentriebwerk
Wir erhalten die Hubfunktionen:
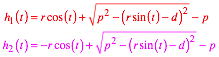
Fr ![]() ,
, ![]() und
und ![]() ergibt sich zum
Beispiel:
ergibt sich zum
Beispiel:
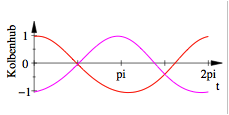
![]() ,
, ![]() und
und ![]()
Im
folgenden Bild mit ![]() ,
, ![]() ,
, ![]() (gr§ere
Desaxierung) und
(gr§ere
Desaxierung) und ![]() (drei
Umdrehungen) sehen wir deutlich, dass die Kurven spiegelbildlich sind mit senkrechten
Spiegelachsen bei
(drei
Umdrehungen) sehen wir deutlich, dass die Kurven spiegelbildlich sind mit senkrechten
Spiegelachsen bei ![]() :
:
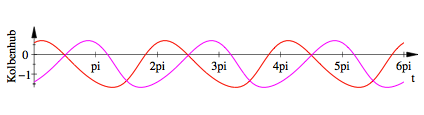
Vertikale Symmetrieachsen
Literatur
[Vogel 2007] Vogel, Jrgen: Stirlingmotor mit Rhombentriebwerk. Maschinen im Modellbau 2/07. S. 12-15