Hans Walser, [20080327a], [20131224]

Kolbenkopf

1 Das Beispiel

Frage: Wo bewegt sich der Kolbenkopf eines Kolbenmotors (Abb. 1) am schnellsten beziehungsweise am langsamsten wenn das Schwungrad sich gleichmäßig dreht? (vgl. [Roth 2008]).

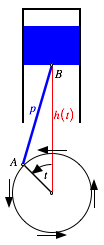
Abb. 1 Kolbenmotor

Eine naheliegende Antwort kann etwa so lauten: Bei der Auf- und Abwärtsbewegung (also für ) ist die Bewegung am schnellsten, um die höchste und tiefste Lage herum am langsamsten.

2 Analyse

Der erste Teil der Antwort ist wegen der unterschiedlichen Schrägstellung der Pleuelstange offensichtlich falsch. Der zweite Teil ist klar („tote Punkte“).

3 Wie ist es nun wirklich?

Wenn wir die Sache so normieren, dass sich der Punkt A auf dem Einheitskreis bewegt, bleibt noch die Länge p der Pleuelstange als Parameter.

Die geneigte Leserin ist eingeladen, vor dem Weiterlesen sich die Dynamik für verschiedene Längen p der Pleuelstange vorzustellen (bewegliches Denken). Besonders interessant sind wie immer die Grenzfälle und ihre Umgebung.

4 Die Rechnung

Für die in der Abbildung 1 eingezeichnete Höhe finden wir:

Der Wurzelausdruck ist der Störefried. Gesucht sind die Extremstellen von , also die Nullstellen von .

5 Beispiele

In den folgenden Diagrammen sind für verschiedene Werte von p jeweils die Grafen von rot, von blau und von grün eingezeichnet.

5.1 p = 2

Für erhalten wir die Diagramme:

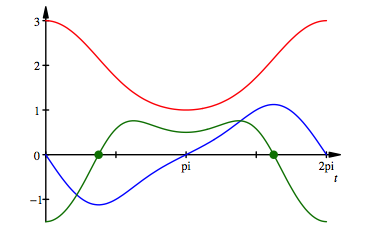
Abb. 2

Die rote Kurve sieht zwar fast wie eine Kosinuskurve aus — der gute Lehrer Lämpel hätte allerdings warnend seinen Zeigefinger erhoben. Schon bei der blauen Kurve wird der Irrtum offensichtlich.

Am schnellsten ist die Bewegung bei

und ,

also auf dem „oberen“ Teil der Kreisbewegung von A.

5.2 p = 1.01

Dies ist nahe beim Grenzfall . Unten durch läuft fast gar nichts.

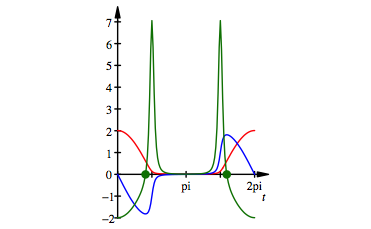
Abb. 3 Fast toter unterer Halbkreis

5.3 p = 1

Nach diesen Vorbereitungen können wir uns nun auch den Grenzfall mit dem toten unteren Halbkreis zu Gemüte führen. Die geneigte Leserin ist eingeladen, sich zu überlegen, ob das sinnvoll ist (bewegliches Denken). Was geschieht, wenn die Trägheit den Kolben durchschießen lässt? Was geschieht bei ? Wie müssen Kurbelwelle und Pleuelstange modifiziert werden? Wie groß ist in diesem Fall der Kolbenhub?

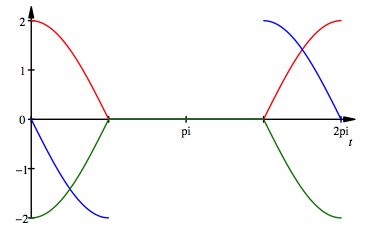
Abb. 4 Toter unterer Halbkreis

5.4 Großes p

Für tendiert die Geschwindigkeitsfunktion gegen und für die Punkte mit schnellster Bewegung gilt und . Das Unzulängliche, hier wird’s Ereignis.

6 Fehleranalyse

Wie kam es zur falschen „Lösung“. Im Folgenden Mutmaßungen.

6.1 Senkrecht statt schräg

Es wurde die „Schrägheit“ der Pleuelstange vernachlässigt. Geometrisch: Verwechslung der Hypotenusenlänge mit einer Kathetenlänge. Der Satz des Pythagoras ist bekannt, aber sein Bildungsgehalt ist noch nicht angekommen.

Pythagoras war ein schräger Vogel. Die deutsche Seele ist senkrecht.

6.2 Blauäugigkeit: Fehler in der Mustererkennung

Für sieht die Bewegungskurve, etwa generiert mit dynamischer Geometrie-Software, auf den allerersten Blick wie eine Kosinuskurve aus.

Diese Ungenauigkeit der Kurvenanalyse hat Tradition: Die Planetenbahnen wurden lange Zeit kreisförmig gesehen, ebenso die Wurfparabel. Man sieht offenbar nur, was man schon kennt. Entdeckendes Lernen ist ein hartes Geschäft.

7 Ausblicke

Wie müsste die Mechanik modifiziert werden, um und zu erhalten?

Gibt es einen geometrisch oder physikalisch einfachen Weg, das Problem zu lösen?

Literatur

[Roth 2008] Roth, Jürgen: Zur Entwicklung und Förderung Beweglichen Denkens im Mathematikunterricht. Eine empirische Längsschnittuntersuchung. JMD, Journal für Mathematik-Didaktik, 29 (2008) Heft 1, S. 20-45