Hans Walser, [20191003]

Kollineare und kozyklische Punkte

1 Worum geht es?

Bearbeitung einer Schulaufgabe (Lehrmittel des Kantons Zürich, Klasse 6, Keller 2016).

2 Beispiel

2.1 Zwölfeck und Punkt

Wir beginnen mit einem regelmäßigen Zwölfeck und einem beliebigen Punkt (Abb. 1).

Abb.1: Zwölfeck und Punkt

2.2 Kreise

Wir zeichnen einen Kreis mit einer Ecke des Zwölfecks als Zentrum durch diesen Punkt (Abb. 2).

Abb. 2: Kreis

Wir zeichnen auch mit allen anderen Ecken des Zwölfecks einen entsprechenden Kreis (Abb. 3). Wir haben nun zwölf Kreise. Sie bilden ein Netz, das aus Kreisvierecken besteht.

Abb. 3: Zwölf Kreise

2.3 Kollineare Punkte

In der Figur der Abbildung 3 entdecken wir exemplarisch sechs kollineare Punkte (Abb. 4). Die Gerade durch diese Punkte geht zusätzlich durch den anfangs gewählten Punkt. Die Gerade ist Diagonale von übereck angeordneten Kreisvierecken.

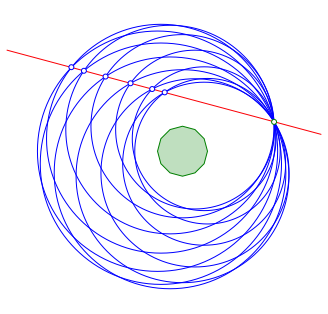
Abb. 4: Kollineare Punkte

2.4 Kopunktale Geraden

Es gibt insgesamt zwölf Geraden durch kollineare Punkte (Abb. 5). Die Geraden schneiden sich unter Winkeln von 15° und Vielfachen davon.

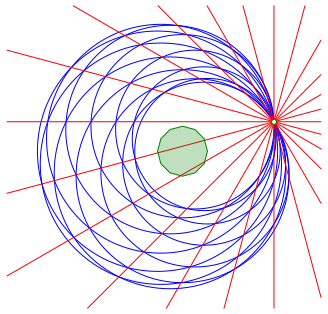
Abb. 5: Geraden durch kollineare Punkte

2.5 Kozyklische Punkte

Wir haben weiter sechs Punkte, die auf einem Kreis liegen (Abb. 6). Der Kreis hat den Mittelpunkt des Zwölfecks als Zentrum und verläuft zusätzlich durch den anfangs gewählten Punkt. Der Kreis ist Kreisdiagonale von übereck angeordneten Kreisvierecken.

Abb. 6: Kozyklische Punkte

Die sechs kozyklischen Punkte bilden ein regelmäßiges Sechseck (Abb. 7).

Abb. 7: Sechseck

2.6 Beweise

In der Abbildung 8 sind zwei der sechs Kreise mit ihren Mittelpunkten hervorgehoben. Sie schneiden sich in zwei Punkten. Der eine Schnittpunkt ist der anfangs gewählte Punkt. Der andere Schnittpunkt ist sein Spiegelbild bei der Spiegelung an der durch die beiden Kreiszentren verlaufenden Geraden.

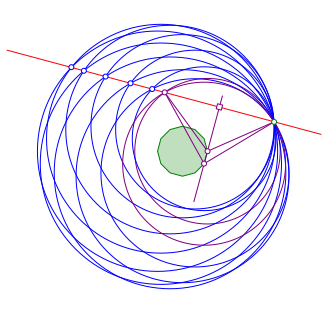
Abb. 8: Spiegelpunkte

In der Abbildung 9 sind die Spiegelachsen für sämtliche der sechs in Frage kommenden Schnittpunkte eingetragen. Da diese Spiegelachsen parallel sind und die sechs in Frage kommenden Schnittpunkte Spiegelbilder desselben anfänglich gewählten Punkte sind, liegen sie auf einer zu den Spiegelachsen senkrechten Geraden durch den anfänglich gewählten Punkt. Damit ist die Kollinearität nachgewiesen.

Abb. 9: Parallele Spiegelgeraden

Die möglichen Spiegelachsen sind Seiten und Diagonalen des Zwölfecks und schließen daher Winkel von 15° und Vielfachen davon ein. Daher tun das auch die Geraden der Abbildung 5.

Die Abbildung 10 zeigt die Spiegelgeraden für die sechs kozyklischen Punkte der Abbildung 6. Diese speziellen Spiegelgeraden sind kopunktal und schließen untereinander Winkel von 30° und Vielfachen davon ein. Daher können die sechs Punkte durch Drehungen um 60° und Vielfache davon aufeinander abgebildet werden. Sie sind somit Eckpunkte eines regelmäßigen Sechsecks.

Abb. 10: Kozyklische Punkte und kopunktale Spiegelgeraden

2.7 Weitere kozyklische Punkte

Nachdem wir den Trick heraus haben, können wir weitere kozyklische Punkte finden.

2.7.1 Vier kozyklische Punkte

Die Abbildung 11 zeigt drei kopunktale Diagonalen im Zwölfeck, die aber nicht durch den Mittelpunkt verlaufen (Walser 2012, S. 29). Die Kopunktalität ergibt sich aus Symmetriegründen. Die drei Diagonalen schneiden sich unter Winkeln von 45° und Vielfachen davon. Wir fokussieren nun auf diejenigen blauen Kreise, die ihre Zentren in den Endpunkten dieser Diagonalen haben. Die beiden Kreise mit dem Zentrum in je einem Ende einer Diagonale schneiden sich im anfangs gewählten Punkt sowie seinem Spiegelpunkt bei Spiegelung an dieser Diagonalen. So erhalten wir zusätzlich zum anfangs gewählten Punkt drei weitere Punkte.

Abb. 11: Kopunktale Diagonalen im Zwölfeck

Diese insgesamt vier Punkte sind kozyklisch (Abb. 12). Das zugehörige Kreiszentrum ist der Schnittpunkt der kopunktalen Diagonalen, also nicht der Mittelpunkt des Zwölfecks. Die vier Punkte sind die Ecken eines Quadrates.

Abb. 12: Kreis und Quadrat

2.7.2 Fünf kozyklische Punkte

Die Abbildung 13 zeigt vier kopunktale Diagonalen im Zwölfeck. Die Kozyklizität ist nicht mehr aus Symmetriegründen trivial (Walser 2012, S. 28). Die Diagonalen schneiden sich unter verschiedenen Winkeln.

Wir erhalten zusammen mit dem eingangs gewählten Punkt fünf kozyklische Punkte. Sie bilden allerdings kein regelmäßiges Fünfeck.

Abb. 13: Fünf kozyklische Punkte

3 Verallgemeinerung

Die Situation kann auf beliebige regelmäßige Vielecke übertragen werden.

3.1 Gerade Eckenzahl

Bei gerader Eckenzahl ist der Sachverhalt völlig analog zum Zwölfeck. Die Abbildung 14 zeigt exemplarisch die Situation im regelmäßigen Achteck.

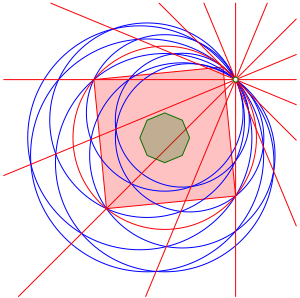
Abb. 14: Regelmäßiges Achteck

Die Abbildung 15 zeigt ein Beispiel von vier kozyklischen Punkten im der Figur.

Abb. 15: Vier kozyklische Punkte

3.2 Ungerade Eckenzahl

Bei ungerader Eckenzahl gibt es ebenfalls kollineare Punkte und kopunktale Geraden (Abb. 16 exemplarisch mit einem regelmäßigen Siebeneck).

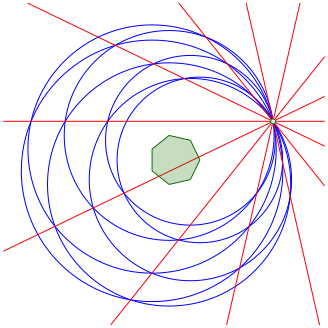
Abb. 16: Regelmäßiges Siebeneck

Hingegen gibt es keine kozyklischen Punkte. Der Kreis (magenta in Abb. 17) um das Zentrum des Siebenecks durch den anfangs gewählten Punkt verläuft zwischen den Schnittpunkten der blauen Kreise. Das hängt damit zusammen, dass sieben nicht durch zwei teilbar ist.

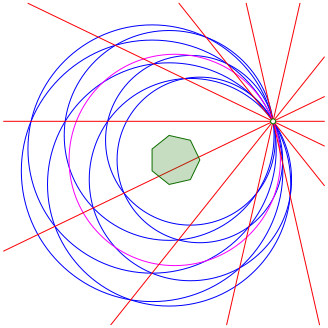
Abb. 17: Magenta Kreis zwischen den Schnittpunkten

Die sieben Schnittpunkte des magenta Kreises mit den blauen Kreisen bilden aber ein regelmäßiges Siebeneck (Abb. 18).

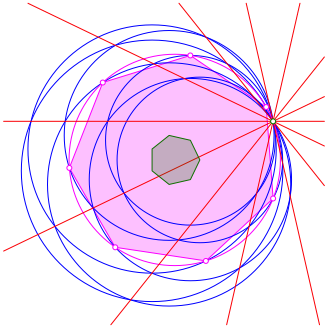
Abb. 18: Regelmäßiges Siebeneck

Literatur

Keller, Bernhard & Keller, Roland & Diener, Marion (2016): Mathematik 6. Lehrmittelverlag Zürich.

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0

Websites

Hans Walser: Schlussstriche

http://www.walser-h-m.ch/hans/Schlussstriche/

Hans Walser: Schnittpunkte

http://www.walser-h-m.ch/hans/Schnittpunkte/