Hans Walser, [20170416]
Kollineare Punkte
1 Der Satz
Zu einem beliebigen Dreieck zeichnen wir den Umkreis (Abb. 1).
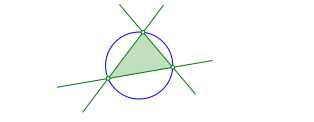
Abb. 1: Umkreis
In den Dreiecksecken zeichnen wir die Tangenten an den Umkreis (Abb. 2).
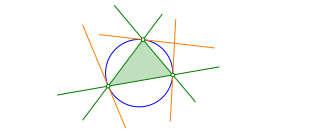
Abb. 2: Tangenten in den Eckpunkten
Wir schneiden jede Tangente mit der dem Berźhrungspunkt gegenźberliegenden Dreiecksseite (oder deren VerlŠngerung) (Abb. 3).
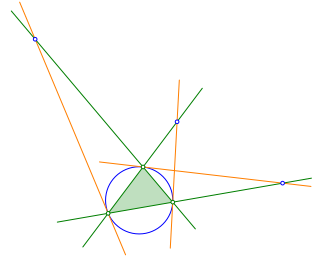
Abb. 3: Schnittpunkte
Die drei Schnittpunkte liegen auf einer Geraden (Abb. 4).
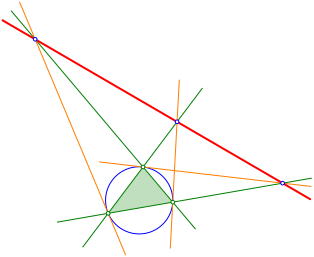
Abb. 4: Kollineare Punkte
2 Der Beweis
Der Satz ist ein Sonderfall des Satzes von Pappos-Pascal.
Der beim Satz von Pappos-Pascal benštigte Kegelschnitt ist der Umkreis des Dreiecks, und je zwei der beim Satz von Pappos-Pascal vorkommenden sechs Punkte auf dem Kegelschnitt sind identifiziert, so dass deren Verbindungsgerade zur Tangente an den Kegelschnitt wird.
3 Fragen
Gibt es einen elementargeometrischen Beweis ohne projektive Geometrie?
Ist der Pol der roten Geraden bezźglich des Umkreises ein ăbesonderer PunktŇ im Dreieck? (vergleiche Abschnitt 5)
Wie ist es beim gleichseitigen Dreieck?
4 Umgekehrt ist auch gefahren
In einem beliebigen Dreieck zeichnen wir den Inkreis (Abb. 5).
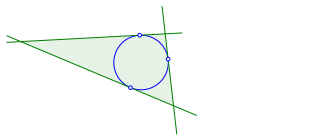
Abb. 5: Inkreis
Die Berźhrpunkte des Inkreises bilden ein Dreieck (Abb. 6).
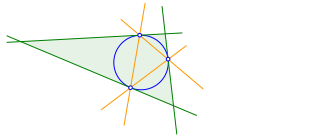
Abb. 6: Berźhrpunktdreieck
Wir schneiden die Seiten des Ausgangsdreiecks mit den Seiten des Berźhrpunktdreiecks gemŠ§ Abbildung 7.
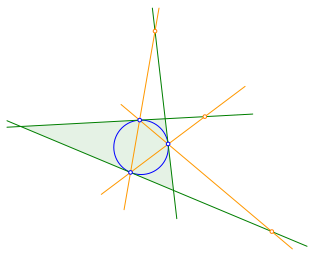
Abb. 7: Schnittpunkte
Die drei Schnittpunkte sind kollinear (Abb. 8).
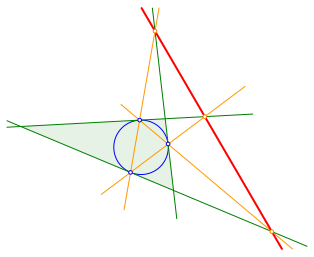
Abb. 8: Kollineare Punkte
Die Figuren der Abbildungen 4 und 8 sind Šquivalent.
5 Der Pol als ăbesonderer PunktŇ
Wir zeichnen den Pol der roten Geraden bezźglich des blauen Inkreises (Abb. 9).
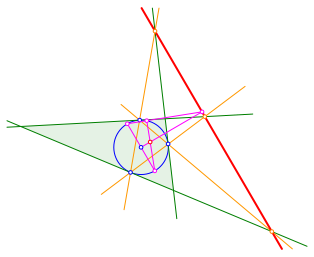
Abb. 9: Pol
Andererseits zeichnen wir die Ecktransversalen des grźnen Dreiecks zu den Berźhrungspunkten des Inkreises (Abb. 10). Diese Ecktransversalen sind kopunktal. Dies kann mit dem Satz von Ceva gezeigt werden.
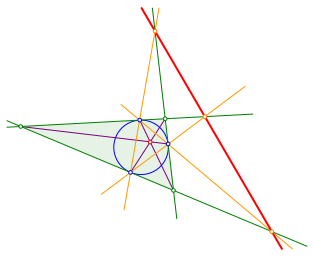
Abb. 10: Transversalenschnittpunkt.
Der Transversalenschnittpunkt ist der Pol (Abb. 11). Mit DGS verifiziert.
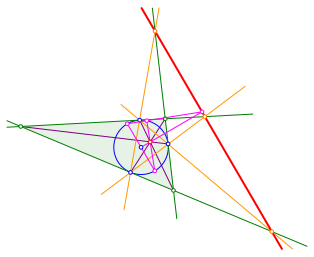
Abb. 11: Der Transversalenschnittpunkt ist der Pol