Hans Walser, [20201109]
Kollineare Punkte
1 Kreisringbögen
Wir beginnen mit drei konzentrischen Kreisringbögen (Abb. 1).
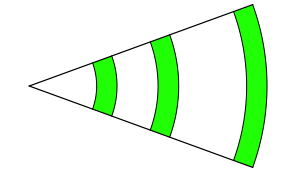
Abb. 1.1: Kreisringbögen
Die drei Kreisringbögen haben dasselbe Zentrum, denselben Öffnungswinkel und die gleiche Dicke. Die drei Innenradien sind beliebig.
Nun zeichnen wir die „Diagonalen“ von links unten nach rechts oben in die Bögen (Abb. 1.2). Ebenso zeichnen wir die Mittelpunkte dieser Diagonalen.
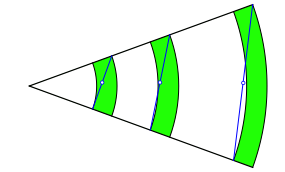
Abb. 1.2: Diagonalen mit Mittelpunkten
Diese Mittelpunkte liegen auf einer Geraden. Sie sind kollinear (Abb. 1.3). Die Gerade geht allerdings nicht durch das gemeinsame Zentrum der Kreisringbögen.
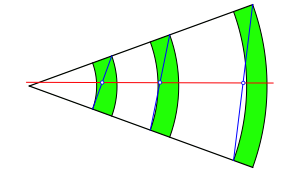
Abb. 1.3: Kollineare Punkte
Wenn wir die Diagonalen in einem anderen Teilverhältnis unterteilen, zum Beispiel im Verhältnis 2:1, ergeben sich ebenfalls kollineare Punkte (Abb. 1.4).
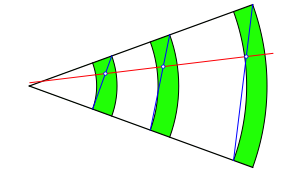
Abb. 1.4: Kollineare Drittelpunkte
2 Beweis
Der Beweis verläuft rechnerisch.
Wir betten die Figur in die Ebene der komplexen Zahlen ein, so dass das Zentrum der Kreisringbögen in den Nullpunkt zu liegen kommt und die untere Sektorgrenze auf die reelle Achse (Abb. 2).
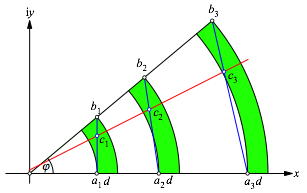
Abb.2: Beweisfigur
Die reellen Zahlen a1, a2 und a3 sind einerseits die Innenradien der Kreisringbögen, andererseits aber auch die Ecken unten links. Die Ringbreite ist d.
Es ist dann:
![]() (1)
(1)
Weiter
ist bei einer Unterteilung im Verhältnis ![]() :
:
![]() (2)
(2)
Einsetzen von (1) in (2) ergibt einen Term von der Form:
![]() (3)
(3)
Um die Kollinearität von c1, c2 und c3 zu zeigen, muss gelten:
![]() (4)
(4)
Einsetzen von (3) in (4) ergibt:
![]() (5)
(5)
Die rechte Seite von (5) ist aber reell. Damit ist die Kollinearität bewiesen.
3 Archimedische Spiralen
Die Abbildung 3 zeigt zwei Beispiele mit archimedischen Spiralen. Wo sind die Kreisringbögen?
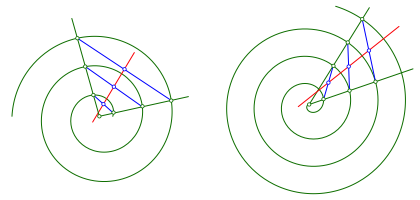
Abb. 3: Archimedische Spiralen
Websites
Hans Walser: Kollineare Punkte
http://www.walser-h-m.ch/hans/Miniaturen/K/Kollineare_Punkte3/Kollineare_Punkte3.htm
Hans Walser: Kollineare Punkte
http://www.walser-h-m.ch/hans/Miniaturen/K/Kollineare_Punkte2/Kollineare_Punkte2.htm
Hans Walser: Kollineare Punkte
http://www.walser-h-m.ch/hans/Miniaturen/K/Kollineare_Punkte1/Kollineare_Punkte1.htm
Hans Walser: Kollineare Punkte
http://www.walser-h-m.ch/hans/Miniaturen/K/Kollineare_Punkte/Kollineare_Punkte.htm
Hans Walser: Kollineare und kozyklische Punkte
http://www.walser-h-m.ch/hans/Miniaturen/K/Koll_kozykl_Punkte/Koll_kozykl_Punkte.htm
Hans Walser: Schlussstriche
http://www.walser-h-m.ch/hans/Schlussstriche/