Hans Walser, [20210118]
Konchoide
1 Worum geht es?
Herleitung einer Konstruktion fŸr die Tangenten und Normalen an eine Konchoide. Dabei wird vorausgesetzt, dass wir die Tangennte und die Normalen an die Leitkurve kennen.
2 Konchoide
Wir gehen von einer Leitkurve mit der Polardarstellung
![]() (1)
(1)
aus. Dabei bezeichnet t den Polarwinkel. Den Pol der Konchoiden legen wir in den Ursprung.
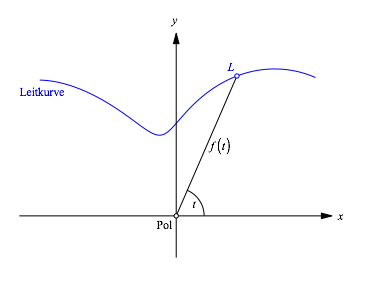
Abb. 1: Leitkurve
Die Konchoide (Abb. 2) mit dem Šu§eren und dem inneren Ast, genannt Konchoide1 beziehungsweise Konchoide2 hat die Polardarstellung:
![]() (2)
(2)
Dabei ist b der vom Pol aus gesehene Abstand der Konchoide von der Leitkurve.
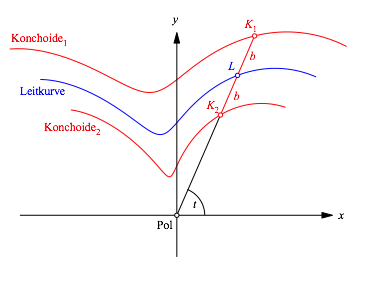
Abb. 2: Konchoide
3 Tangenten und Normalen
Zur Berechnung der Tangenten und Normalen verwenden wir die aus (1) und (2) abgeleiteten kartesischen Darstellungen.
FŸr die Leitkurve also:
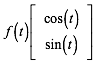 (3)
(3)
Somit hat die Leitkurve den Tangentialvektor
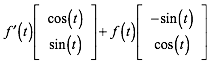 (4)
(4)
und den Normalvektor:
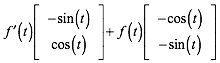 (5)
(5)
FŸr die Konchoide ergibt sich die kartesische Darstellung:
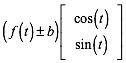 (6)
(6)
FŸr den Tangentialvektor erhalten wir
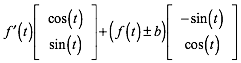 (7)
(7)
und fŸr den Normalvektor:
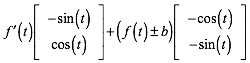 (8)
(8)
4 Ein Schnittpunkt
Die Normalvektoren der Leitkurve und der Konchoide haben dieselbe erste Komponente. Die zweite Komponente ist das Negative der jeweiligen Polardarstellung.
Damit ergibt sich die Stimmigkeit der Abbildung 3.
Die Normalen an Leitkurve und Konchoide sowie die Normale zur Polgerade mit dem Steigungswinkel t haben den Punkt N gemeinsam.
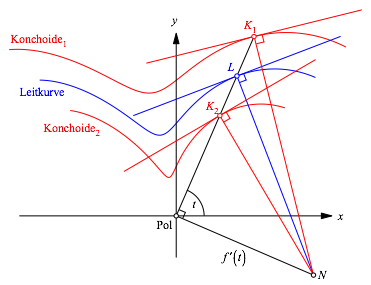
Abb. 3: Gemeinsamer Schnittpunkt der Normalen
5 Konstruktives Vorgehen
Wir beginnen mit Tangente und Normale der Leitkurve, deren Kenntnis wir vorausgesetzt haben. Damit kšnnen wir den Punkt N konstruieren (Abb. 4).
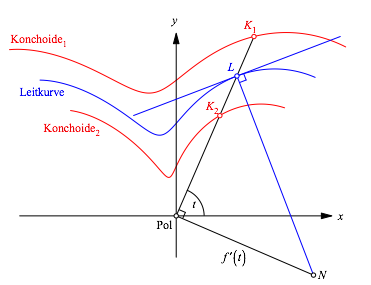
Abb. 4: Erster Schritt
Anschlie§end kšnnen wir Normalen und Tangenten an die Konchoide konstruieren gemŠ§ Abbildung 3.
6 Beispiele
6.1 Konchoide von Nikomedes
Die Leitkurve ist eine Gerade (Abb. 5). Daher kšnnen Normale und Tangente mit elementaren Mitteln gezeichnet werden.
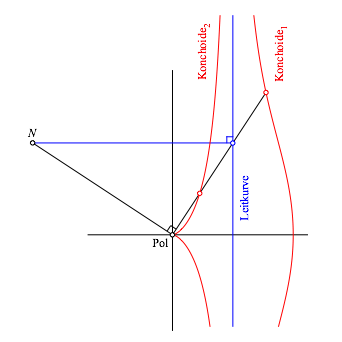
Abb. 5: Nikomedes. Erster Schritt
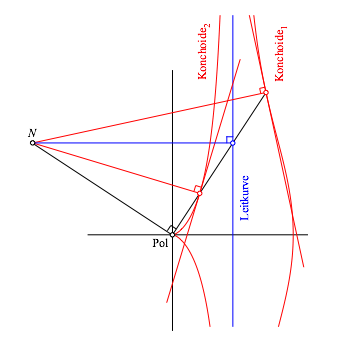
Abb. 6: Normalen und Tangenten
6.2 Pascalsche Schnecke
Bei der Pascalschen Schnecke (Abb. 7) (ƒtienne Pascal, 1588-1651, Vater von Blaise Pascal) ist die Leitkurve ein Kreis. Daher kšnnen Normale und Tangente mit elementaren Mitteln gezeichnet werden. Die Šu§ere und die innere Konchoide schlie§en zu einer durchgehenden Kurve. Die †bergangsstellen sind auf der Senkrechten zur Symmetrieachse durch den Pol.
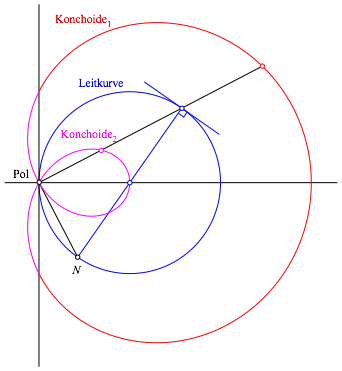
Abb. 7: Pascalsche Schnecke. Erster Schritt
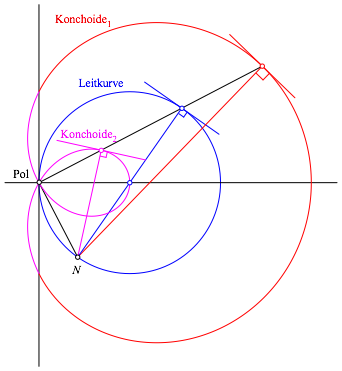
Abb. 8: Normalen und Tangenten
6.3
Archimedische Spirale
Die
archimedische Spirale (Abb. 9) ist eine Konchoide mit sich selbst als Leitkurve
(SelbstkonchoidalitŠt). Bei der Frage nach Normalen
und Tangenten ist somit die Lšsung das Problem.
Wir
kšnnen aber rechnerisch vorgehen. Wir verwenden die Polargleichung:
![]() (9)
(9)
Damit ist:
![]() (10)
(10)
Das ist der
Abstand des Punktes N vom Pol.
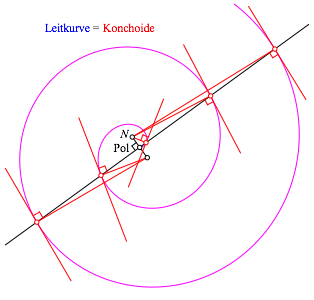
Abb.
9: Archimedische Spirale