Hans Walser, [20100915a]
Die kopernikanische Wende
Anregungen: A. F., B. und M. S., F.
1 Worum geht es?
Es werden zwei Beispiele elementarer Bewegungs-Aufgaben vorgestellt, bei denen ein Perspektivenwechsel zu einer einfacheren Lsung fhrt.
2 Historisches
Im geozentrischen Weltbild, das Ptolemus im Almagest vorstellte, wurden etwa 80 Epizykel bentigt, um die Planetenbahnen auf (berlagerte) Kreisbewegungen zurckzufhren. Der Wechsel zum heliozentrischen Weltbild durch Kopernikus vereinfachte die Beschreibung der Planetenbahnen (vgl. [Wu§ing 2010], S. 51-54).
3 Beispiele aus der Bewegungsgeometrie
3.1 Die abrutschende Leiter
An einer Hauswand steht eine schrg angelehnte Leiter AB. Wo bewegt sich der Mittelpunkt M dieser Leiter, wenn sie abrutscht?
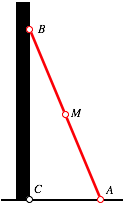
Schrge Leiter
Im geozentrischen Weltbild bleiben Boden und Hauswand fest, whrend sich die Leiter und damit der Punkt M bewegen. Gesucht ist die Bahnkurve des Punktes M relativ zu Boden und Wand.
Wir ndern nun die Perspektive und gehen zu einem leiterzentrischen Weltbild ber. Die Leiter bleibt also fest. Hingegen bewegen sich Boden und Hauswand. Illustration: Ein Kiltbub befindet sich auf halber Leiterhhe, da beginnt die Leiter zu rutschen. Er klammert sich an die Leiter und sieht durch die Sprossen hindurch, wie ihm die Hauswand auf den Kopf zu fallen droht. Und oben lacht das Mdi zum Fenster heraus.
Der Fu§punkt C der Wand bewegt sich auf dem Thaleskreis ber der Leiter AB. Dieser Thaleskreis hat das Zentrum M. Der Abstand CM ist also konstant und ist gleich der halben Leiterlnge.
3.2 Der wegrollende Inkreis
Von einem Dreieck ABC seien die Eckpunkte A und B fixiert, ebenfalls ist der Inkreisradius gegeben. Auf welcher Kurve bewegt sich die Ecke C, wenn der Inkreis auf der Grundseite AB hin und her rollt?
Wir
arbeiten exemplarisch mit den Daten: ![]() ,
, ![]() und dem Inkreisradius
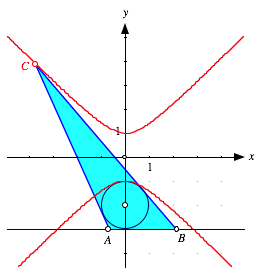
1. Die Abbildung zeigt, welche Ortslinie sich mit DGS (Cabri) fr C ergibt.
und dem Inkreisradius
1. Die Abbildung zeigt, welche Ortslinie sich mit DGS (Cabri) fr C ergibt.
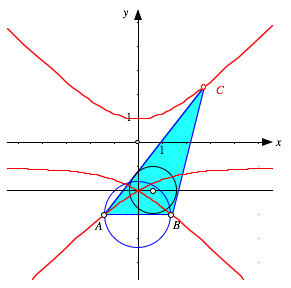
Geozentrische Sicht der Ortslinie
Der obere Ast der Kurve sieht scheinbar nach Hyperbel aus, im unteren Ast, der seinerseits aus zwei Teilen besteht, werden wir eines anderen belehrt. Mit diesem unteren Ast hat es folgendes auf sich: Solange der Inkreismittelpunkt sich im Innern des in der Abbildung eingezeichneten Thaleskreises ber AB befindet, haben wir einen Inkreis. Wenn aber der Inkreismittelpunkt aus diesem Bereich herausrollt, mutiert der Kreis zu einem Ankreis. Dies kann mit Winkelberlegungen gezeigt werden. Der Punkt C liegt dann auf dem unteren Ast. Im Grenzfall mit dem Inkreiszentrum auf dem Thaleskreis ergeben sich zwei parallele Trgergeraden fr die Dreiecksseiten a und b. Der Punkt C ist dann ein uneigentlicher Punkt. Daher die Asymptoten der Kurve.
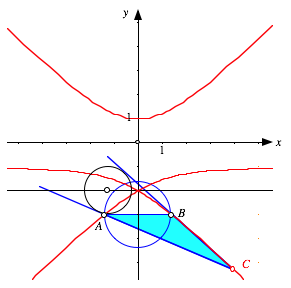
Ankreis
Die
Ortskurve kann wie folgt parametrisiert werden. Als Parameter t verwenden wir die x-Koordinate des Inkreismittelpunktes. Dieser hat also die
Koordinaten ![]() . Damit erhalten wir die Dreieckswinkel:
. Damit erhalten wir die Dreieckswinkel:

Nun knnen wir fr die Ecke C einen Vorwrtseinschnitt machen. Fr die Hhe h des Dreieckes ABC und den von A ausgehenden Abschnitt p bis zu Hhenfu§punkt ergeben sich:
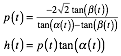
Unter Bercksichtigung der Koordinaten von A und B erhalten wir fr die Kurve die Parametrisierung:
![]()
Die Abbildung zeigt die CAS-generierte Kurve.
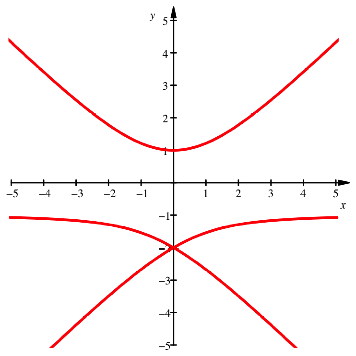
Kurve
Fr ![]() ergibt sich der
obere Ast, fr
ergibt sich der
obere Ast, fr ![]() beziehungsweise
beziehungsweise ![]() ergeben sich die
beiden Teile des unteren Astes. Fr
ergeben sich die
beiden Teile des unteren Astes. Fr ![]() erhalten wir uneigentliche
Punkte. Die Kurve ist zwar schn, aber keine Hyperbel.
erhalten wir uneigentliche
Punkte. Die Kurve ist zwar schn, aber keine Hyperbel.
Nun machen wir wiederum die kopernikanische Wende, indem wir den Inkreis festhalten und die Strecke AB unter Beibehaltung ihrer Lnge unter dem Inkreis horizontal hin und her rutschen lassen.
Dann ergibt sich als Ortslinie fr C die (gleichseitige) Hyperbel mit der Gleichung:
![]()
Die Gleichseitigkeit der Hyperbel ist nicht spezifisch fr die Aufgabe, sondern ergibt sich aus den gewhlten Anfangsdaten.
Inkreiszentrische Sicht der Ortskurve: Hyperbel
Im
Unterricht kann das so verifiziert werden, dass wir mit der Hyperbel beginnen,
auf der Hyperbel einen variablen Punkt C
whlen und dann die Lnge des Schlagschattens des festen Inkreises auf die
Gerade ![]() bei
Zentralbeleuchtung von C aus messen.
Seine Lnge AB ist konstant
bei
Zentralbeleuchtung von C aus messen.
Seine Lnge AB ist konstant ![]() .
.
Fr C auf dem unteren Ast erhalten wir die Ankreis-Situation.
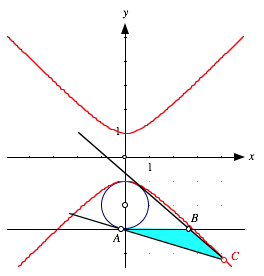
Ankreis
Aus der
inkreiszentrischen Konstruktion ergibt sich folgende Parametrisierung der Kurve.
Den Parameter t whlen wir so, dass
der Punkt ![]() der Mittelpunkt
der Strecke AB ist. Dann ist:
der Mittelpunkt
der Strecke AB ist. Dann ist:
Weiter ist:
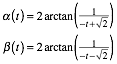
Weiter wie im geozentrischen Fall:
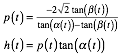
Unter
Bercksichtigung der Koordinaten von ![]() und
und ![]() erhalten wir fr
die Kurve die Parametrisierung:
erhalten wir fr
die Kurve die Parametrisierung:
![]()
Die
Abbildung zeigt rot die CAS-generierte Kurve. Zu Vergleichszwecken wurde die
durch ![]() generierte
Hyperbel in gelb unterlegt.
generierte
Hyperbel in gelb unterlegt.
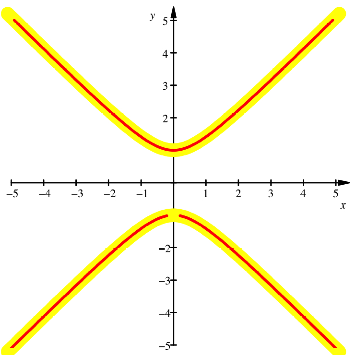
Hyperbel
Wer Lust hat, kann die formalen Beweise nachliefern, mglichst fr den allgemeinen Fall.
Literatur
[Wu§ing 2010] Wu§ing, Hans: Von Leonardo da Vinci bis Galileo Galilei. EAGLE-GUIDE. EAGLE 041. Leipzig: Edition am Gutenbergplatz Leipzig 2010. ISBN 978-3-937219-41-7.