Hans Walser, [20150129]

Kopunktale Geraden

1 Worum geht es?

In der Schule lernt man, dass sich die drei Schwerlinien eines Dreieckes in einem Punkt schneiden, dem Schwerpunkt. Wir fragen nun umgekehrt: Wie findet man zu drei Geraden, die sich in einem Punkt schneiden (so genannte kopunktale Geraden) ein passendes Dreieck mit den drei gegebenen Geraden als Schwerlinien?

Analoge Frage für weitere spezielle Punkte im Dreieck.

Die Lösungen sind immer nur bis auf Ähnlichkeit machbar.

Die Lösungen basieren auf Schließungsfiguren und lassen Verallgemeinerungen zu.

2 Schwerpunkt und Schwerlinien

Gegeben sind drei Geraden mit einem gemeinsamen Schnittpunkt S (Abb. 1). Gesucht ist ein passendes Dreieck .

Abb. 1: Schwerlinien vorgegeben

Wir wählen den Punkt auf und ergänzen zum Parallelogramm gemäß Abbildung 2.

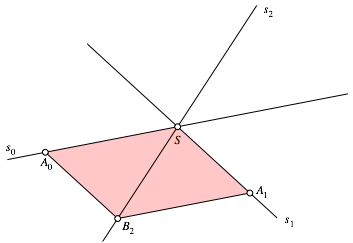
Abb. 2: Parallelogramm einpassen

Nun fügen wir ein zweites und ein drittes Parallelogramm gemäß Abbildung 3 ein. Wir erhalten eine Schließungsfigur. Das Dreieck löst unser Problem, ebenso das Dreieck . Der Nachweis ergibt sich dadurch, dass sich die Diagonalen im Parallelogramm gegenseitig halbieren.

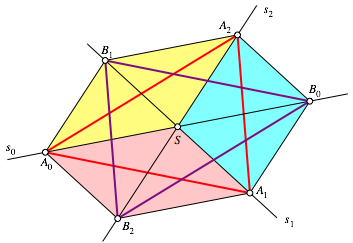
Abb. 3: Lösungen

3 Höhen und Mittelsenkrechte

3.1 Höhen

Wir wählen den Punkt auf (Abb. 4) und fällen das Lot auf . Der Schnittpunkt der Lotgeraden mit ist .

Abb. 4: Höhen gegeben

Entsprechend fahren wir weiter und erhalten eine Schließungsfigur, welche das Problem löst (Abb. 5).

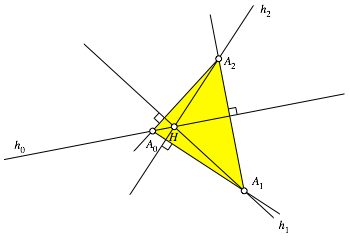
Abb. 5: Lösung

3.2 Mittelsenkrechte

Mittelsenkrechte und Mittelsenkrechtenschnittpunkt eines Dreieckes sind zugleich Höhen und Höhenschnittpunkt im zugehörigen Kantenmittendreieck. Wir konstruieren daher zunächst analog zum Vorgehen in der Abbildung 5 das Kantenmittendreieck und ergänzen dieses zum Dreieck (Abb. 6).

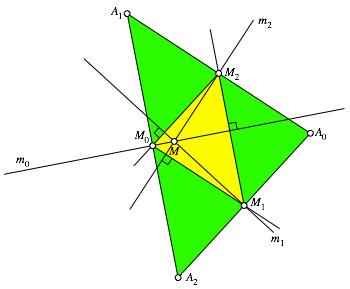
Abb. 6: Mittelsenkrechte

4 Winkelhalbierende

Dazu brauchte ich etwas Rechnung. An den Ecken haben wir die entsprechenden Dreieckwinkel . Weiter führen wir die drei Winkel gemäß Abbildung 7 ein.

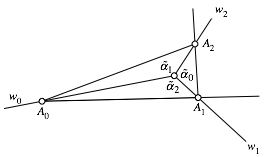
Abb. 7: Bezeichnungen

Mit diesen Bezeichnungen ist:

Wegen ergibt sich:

Somit ist:

Daher ergibt sich folgende Konstruktion: Wir subtrahieren von einen rechten Winkel und erhalten so . Diesen Winkel tragen wir in einem auf gewählten Punkt ab (Abb. 8).

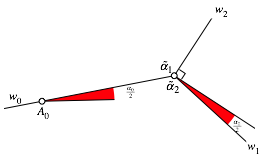
Abb. 8: Halber Dreieckswinkel

Damit können wir konstruieren und durch Weiterspiegeln (Abb. 9). Wir haben erneut eine Schließungsfigur.

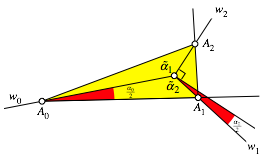
Abb. 9: Konstruktion des Dreieckes

5 Verallgemeinerungen

5.1 Schließungsfigur mit Parallelogrammen

Das entspricht der Lösung bei drei kopunktalen Geraden, welche Schwerlinien werden sollen.

5.1.1 Vier kopunktale Geraden

Mit vier kopunktalen Geraden erhalten wir keine Schließungsfigur, sondern eine Spirale (Abb. 10). In welchen Sonderfällen gibt es trotzdem eine Schließungsfigur?

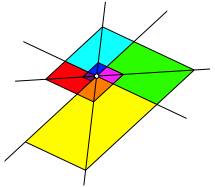
Abb. 10: Spirale bei vier kopunktalen Geraden

5.1.2 Fünf kopunktale Geraden

Bei fünf kopunktalen Geraden ergibt sich eine Schließungsfigur (Abb. 11a).

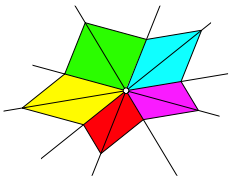
Abb. 11a: Schließungsfigur

Für den Beweis der Schließungseigenschaft verwenden wir die Bezeichnungen der Abbildung 11b.

Abb. 11b: Bezeichnungen

Wir verwenden den Sinussatz in den halben Parallelogrammen. Zunächst ist:

Analog finden wir:

Man beachte den Paritätssprung nach der ersten halben Runde. Dieser Paritätssprung tritt immer bei einer ungeraden Zahl von Geraden auf.

Nun können wir einsetzen und kürzen:

Der Paritätssprung erlaubt das vollständige Kürzen. Wegen schließt sich die Figur.

Man kann die Figur mit weiteren Parallelogrammen zu einer „schönen“ Figur ergänzen (Abb. 12).

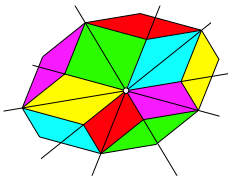
Abb. 12: Ergänzung mit weiteren Parallelogrammen

Die nächste Runde von Parallelogrammen geht nach innen (Abb. 13).

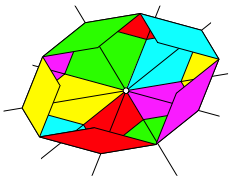
Abb. 13: Weitere Parallelogramme

Und schließlich schließt sich die Figur (Abb. 14).

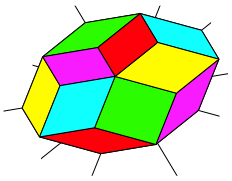
Abb. 14: Schließungsfigur

5.1.3 Sechs kopunktale Geraden

Bei sechs kopunktalen Geraden ergibt sich wieder eine Spirale (Abb. 15).

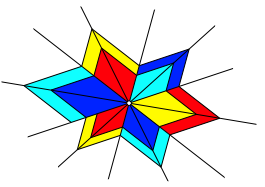
Abb. 15: Sechs kopunktale Geraden

5.1.4 Sieben kopunktale Geraden

Bei sieben kopunktalen Geraden ergibt sich wieder eine Schließungsfigur (Abb. 16), die wir mit weiteren Parallelogrammen ergänzen können (Abb. 17).

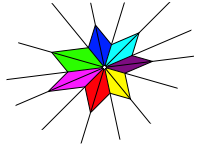
Abb. 16: Sieben kopunktale Geraden

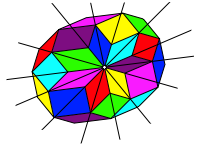
Abb. 17: Ergänzung mit Parallelogrammen

5.1.5 Paritätsproblem

Offenbar gibt es bei einer ungeraden Anzahl von Geraden eine Schließungsfigur, bei einer Geraden Anzahl eine Spirale.

5.2 Schließungsfigur mit Orthogonaltrajektorien

Es ergibt sich wieder der Paritätsunterschied.

5.2.1 Gerade Anzahl kopunktaler Geraden

Wir erhalten im Regelfall eine Spirale (Abb. 18).

Abb. 18: Spirale

5.2.2 Ungerade Anzahl kopunktaler Geraden

Nun ergibt sich eine Schließungsfigur. Der Beweis kann mit Trigonometrie erbracht werden (Walser 2011, S. 32, 33, 70-72).

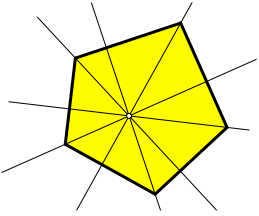
Abb. 19: Schließungsfigur

5.3 Schließungsfiguren mit Spiegelungen

Wir beginnen mit einer Geraden mit einem beliebigen Winkel zu einer der drei vorgegebenen kopunktalen Geraden und spiegeln dann fortlaufend an den kopunktalen Geraden.

Es zeigt sich wiederum eine Paritätsunterscheidung.

5.3.1 Ungerade Anzahl Geraden

Wir haben eine Schließungsfigur mit einer Periodenlänge, die doppelt so groß wie die Anzahl der Geraden ist. Die Abbildung 20 zeigt die Situation bei drei Geraden.

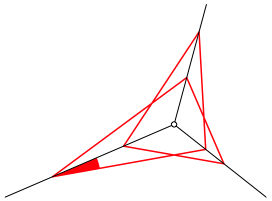
Abb. 20: Drei Geraden

Die Schließungseigenschaft ergibt sich daraus, dass die sukzessive Spiegelung an einer ungeraden Anzahl kopunktaler Geraden auf eine einzige Geradenspiegelung reduziert werden kann. Zweimalige Anwendung dieser Abbildung ist dann die Identität.

Die Figur hat einen Inkreis (Abb. 21).

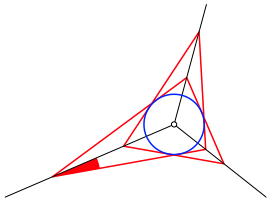
Abb. 21: Inkreis

5.3.2 Gerade Anzahl Geraden

Die sukzessive Spiegelung an einer geraden Anzahl kopunktaler Geraden ist eine Drehung um den gemeinsamen Schnittpunkt. Der Drehwinkel ist das Doppelte der Summe von Schnittwinkeln aufeinanderfolgender Geradenpaare. Falls der Drehwinkel in einem rationalen Verhältnis zum vollen Winkel steht, haben wir eine Schließungsfigur, sonst nicht. Im Regelfall also nicht. Die Abbildung 22 zeigt den einfachsten Fall mit zwei Geraden. Die Figur hat einen Inkreis.

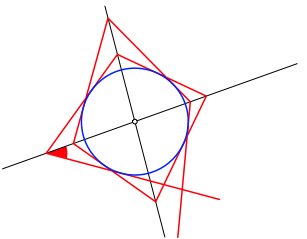
Abb. 220:Schließungsfigur?

Literatur

Walser, Hans (2011): Geometrische Miniaturen. Figuren – Muster – Symmetrien. Leipzig. EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-42-4.