Hans Walser, [20200128]
Kosinus-Approximationen
1 Worum geht es?
Fźr die Herleitung der Ableitung der Sinus-Funktion benštigt man den Grenzwert:
![]() (1)
(1)
Der Trick besteht darin, die Kosinus-Funktion geeignet zu approximieren, um den Grenzwert zu bestimmen.
ZunŠchst aber das Vorgehen zur Ableitung.
2 Ableitung der Sinus-Funktion
Wir bilden den Differentialquotienten:
![]() (2)
(2)
Umformung mit dem Additionstheorem:
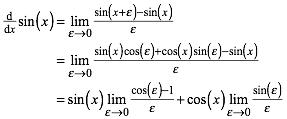 (3)
(3)
Mit einer separaten †berlegung wird im Unterricht gezeigt:
![]() (4)
(4)
Wir haben noch (1) zu berechnen.
3 Approximationen
Als Approximation der Kosinus-Funktion in einer Umgebung von x = 0 bieten sich an (die Farben beziehen sich auf die Grafen dieser Funktionen in der Abbildung 1):
 (5)
(5)
3.1 Funktionsgrafen
In der Abbildung 1 ist die Kosinus-Kurve rot eingezeichnet, die Grafen der Approximationen gemŠ§ den in (5) angegebenen Farben.
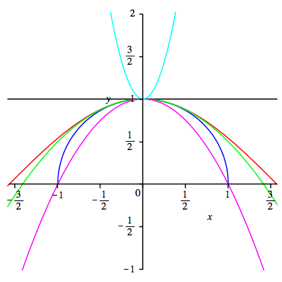
Abb. 1: Funktionsgrafen
Der optische Befund zeigt, dass die Funktionen d und e die Kosinus-Kurve in der NŠhe der Stelle x = 0 recht gut approximieren, die anderen sind weniger gut.
3.2 Funktionswerte
Die Tabelle 1 zeigt die Funktionswerte in der NŠhe der Stelle x = 0.
|
x |
cos(x) |
c(x) |
d(x) |
e(x) |
f(x) |
g(x) |
|
0.2 |
0.9800665778 |
1 |
0.9797958971 |
0.980 |
0.96 |
1.28 |
|
0.02 |
0.9998000067 |
1 |
0.9997999800 |
0.9998000000 |
0.9996000000 |
1.002800000 |
|
0.002 |
0.9999980000 |
1 |
0.9999980000 |
0.9999980000 |
0.9999960000 |
1.000028000 |
|
0.0002 |
0.9999999800 |
1 |
0.9999999800 |
0.9999999800 |
0.9999999600 |
1.000000280 |
|
0.00002 |
0.9999999998 |
1 |
0.9999999998 |
0.9999999998 |
0.9999999996 |
1.000000003 |
|
0.000002 |
1.000000000 |
1 |
1. |
1. |
1. |
1.000000000 |
Tab. 1: Funktionswerte
Wir sehen auch hier, dass die Funktionen d und e deutlich besser sind als die anderen.
3.3 Grenzwert
Das Interessante ist, dass die Gźte der Approximation keinen Einfluss auf den Grenzwert (1) hat. Wir zeigen das an der spinnerten ăApproximationŇ mit g, der nach oben offenen Parabel. Es ist:
![]() (6)
(6)
Denselben Grenzwert 0 erhalten wir auch mit den anderen Approximationen. Am einfachsten ist es natźrlich, mit der konstanten Funktion c zu arbeiten.
Der Witz
der Sache ist, dass wir in den Approximationen keinen linearen Anteil in ![]() haben. Und
der quadratische Anteil fźhrt zum Grenzwert null.
haben. Und
der quadratische Anteil fźhrt zum Grenzwert null.
Somit erhalten wir aus (3) fźr die Ableitung der Sinus-Funktion:
![]() (7)
(7)
In (7) wird x im Bogenma§ verwendet. Bei anderen Winkelma§en kommt ein Korrekturfaktor als innere Ableitung (Kettenregel) dazu.
4 Kommentar zu den Approximationen
Die Approximation mit der konstanten Funktion c ist sozusagen die Primitivlšsung, die aber fźr unsere Zwecke všllig ausreicht.
Fźr die Approximation d hŠngen wir an die Approximation fźr den Sinus fźr kleine x-Werte an:
![]() (8)
(8)
Daraus ergibt sich:
![]() (9)
(9)
Dies ist die Approximation d. Sie ist nur reell fźr –1 ˛ x ˛ +1. Der Funktionsgraf ist die obere HŠlfte des Einheitskreises. Dieser Kreis ist der Krźmmungskreis der Kosinus-Kurve an der Stelle x = 0.
Aus d erhalten wir e mit dem ăschmutzigen Trick von NewtonŇ (Schźlerausdruck). Wir
fźgen unter der Wurzel von (9) noch den Ausdruck ![]() ein.
Dieser Ausdruck ist als vierte Potenz gegenźber dem quadratischen Anteil vernachlŠssigbar
klein.
ein.
Dieser Ausdruck ist als vierte Potenz gegenźber dem quadratischen Anteil vernachlŠssigbar
klein.
Somit haben wir:
![]() (10)
(10)
Dies ist die Approximation e.
Bemerkung: Diese Approximation ist das Taylor-Polynom zweiten Grades der Kosinus-Funktion. Wir haben es jetzt aber ohne Differentialrechnung hergeleitet. Sie ist die beste quadratische Approximation der Kosinus-Funktion in der NŠhe von x = 0. Sie hat an der Stelle x = 0 dieselbe Krźmmung wie die Kosinus-Kurve.
Die Approximationen f und g dienen nur zur Illustration, dass in unserem Kontext der quadratische Anteil gar nicht nštig ist.