Hans Walser, [20170718]
Kosinusspindel
Indirekte Anregung: F. H., B.
1 Worum geht es?
RotationsflŠche mit einer Kosinuskurve als Meridian.
2 Parameterdarstellungen
2.1 Einheitskugel
Wir gehen aus von der klassischen Parameterdarstellung der Einheitskugel (Abb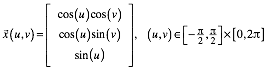. 1):
(1)
Abb. 1: Einheitskugel
2.1.1 Erinnerung an die Schule
Die
Einheitskugel hat das Volumen 
, die OberflŠche 
und die
MeridianflŠche (halbe AchsenschnittflŠche) 
.
2.2 Kosinusspindel
Wir Šndern die Parameterdarstellung (1) wie folgt:
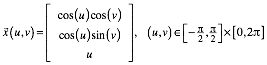(2)
Dies fŸhrt zur FlŠche der Abbildung 2.
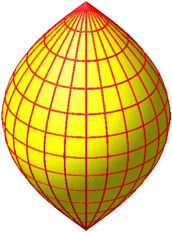
Abb. 2: Kosinusspindel
Die
Kosinusspindel hat die Kosinuskurve fŸr 
als
Meridian. Daher der Name (ad hoc Bezeichnung).
Die Abbildung 3 zeigt die Relation zur Einheitskugel.
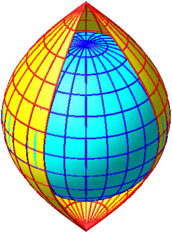
Abb. 3: Relation zur Einheitskugel
3 SchulmŠ§ige Berechnungen
3.1 Volumen
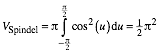(3)
Die
ãschšneÒ Formel fŸhrt zur Frage, ob es weitere Figuren
gibt, deren Volumenformel aus 
mit einem
rationalen Koeffizienten besteht.
Dies ist zum Beispiel beim Torus der Fall.
Die
Gesamtfigur der Abbildung 4 hat das Volumen 
.
Abb. 4: Torus und Kosinusspindel
3.2 OberflŠche
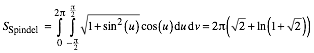(4)
Leider kein ãschšnesÒ Resultat.
3.3 MeridianflŠche
(5)
4 Schraubenlinie
4.1 Auf SpindelflŠche
Die Abbildung 5a zeigt eine Schraubenlinie (rot), die auf die SpindelflŠche passt (Abb. 5b). Nachweis durch Rechnung.
Die
Schraubenlinie hat den Radius 
und die Ganghšhe 
. Sie ist also eine auf 50% skalierte Kopie der
Standard-Schraubenlinie mit Radius 1 und Ganghšhe 
. GegenŸber der Horizontalebene hat sie die Steigung
1, also den Steigungswinkel 45¡.
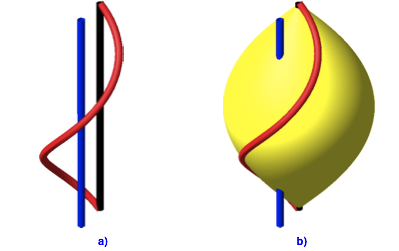
Abb. 5: Spirale auf der Spindel
Die schwarze Spindelachse und die blaue Achse der roten Schraubenlinie sind verschieden. Die schwarze Spindelachse verbindet Anfang und Ende der Schraubenlinie.
Die rote Schraubenlinie passt auf drei weitere FlŠchen. Nachweise durch Rechnung.
4.2 Auf Zylinder
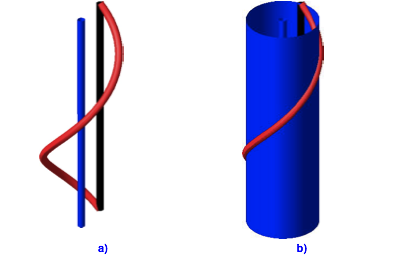
Abb. 6: Schraubenlinie auf Zylinder
Die Schraubenlinie passt auf einen Zylinder (Abb. 6, blau), welcher dieselbe Achse hat wie die Schraubenlinie. Die schwarze Spindelachse ist eine Mantellinie des Zylinders.
4.3 Auf SchraubenflŠche
Abb. 7: Schraubenlinie auf SchraubenflŠche
Die Schraubenlinie
passt auf eine SchraubenflŠche (Abb. 7, grŸn), welche die schwarze Spindelachse
als Achse hat. Dies ist verblŸffend. Die SchraubenflŠche hat die Ganghšhe 
.
4.4 Auf zweiter SchraubenflŠche
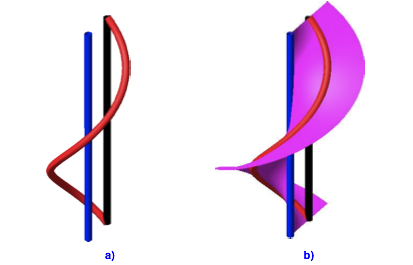
Abb. 8: Triviale SchraubenflŠche
Die
Schraubenlinie liegt trivialerweise auf der ãeigenenÒ SchraubenflŠche (Abb. 8, magenta). Diese SchraubenflŠche hat wie die rote
Schraubenlinie die Ganghšhe 
.
Wegen der konstanten Steigung 1 unserer Schraubenlinie ist sie auf den betrachteten FlŠchen jeweils eine Bšschungslinie (Kurve konstanten Anstieges).
5 Schnittkurve
Die rote Schraubenlinie ist also Schnittkurve beim Schnitt von zwei oder mehreren der obigen FlŠchen (Abb. 9 bis #).
5.1 Spindel und Zylinder
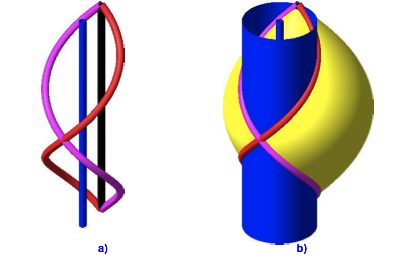
Abb. 9: Spindel und Zylinder
5.2 Spindel und SchraubenflŠche
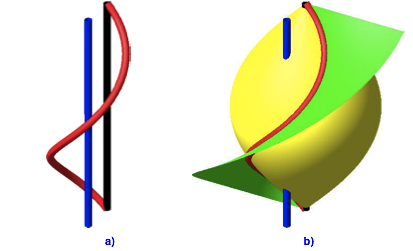
Abb. 10: Spindel und SchraubenflŠche
5.3 Spindel und SchraubenflŠche
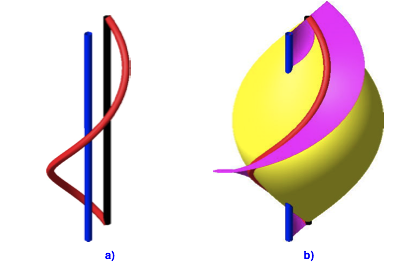
Abb. 11: Spindel und SchraubenflŠche
5.4 Zylinder und SchraubenflŠche
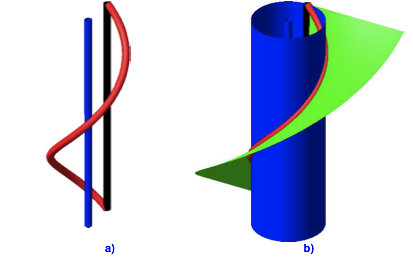
Abb. 12: Zylinder und SchraubenflŠche
5.5 Zylinder und SchraubenflŠche
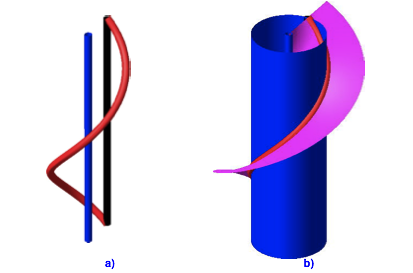
Abb. 13: Zylinder und SchraubenflŠche
5.6 SchraubenflŠche und SchraubenflŠche
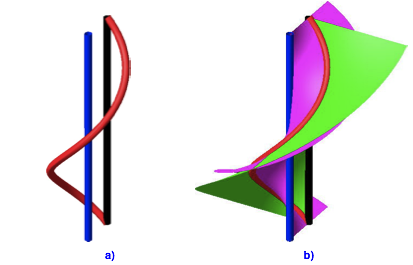
Abb. 14: Zwei SchraubenflŠchen
Abb. 15: Sicht von oben
Abb. 16: Sicht von allen Seiten
5.7 Synopsis
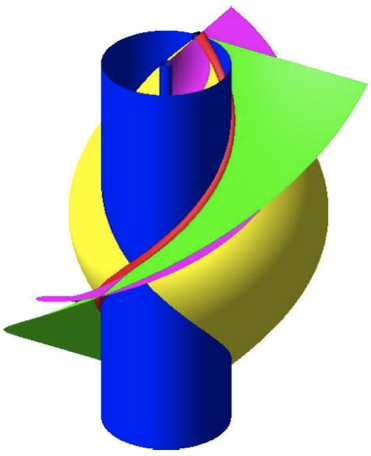
Abb. 17: Synopsis
6 Mehrere Schraubenlinien
In der Abbildung 18a ist die Kosinusspindel mit den Parameterlinien gemŠ§ der Parametrisierung (2) (siehe auch Abb. 2 und 3) eingezeichnet. Unsere Schraubenlinie ist offensichtlich eine Diagonalkurve der Parametrisierung. In der Abbildung 18b sind weitere diagonale Schraubenlinien eingezeichnet.
Die Kosinusspindel kann also auch mit der Schraubenlinie als Meridian erzeugt werden.
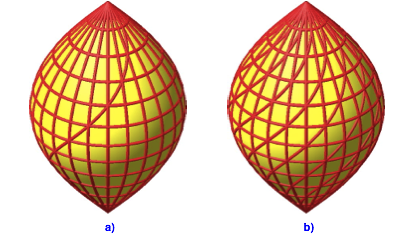
Abb. 18: Netzlinien und Spiralen
Die Abbildung 19a enthŠlt nur noch die Spiralen. In der Abbildung 19b sind zusŠtzlich die Konterspiralen eingezeichnet.
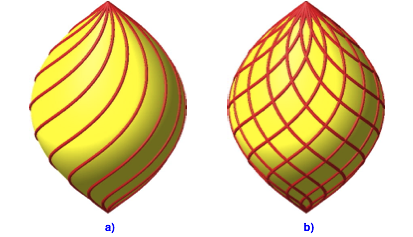
Abb. 19: Spiralen und Konterspiralen
Die Abbildung 20 zeigt einen eisernen Pfahlabschluss (Arabal, Kashmir). Er erinnert an die Abbildung 19a. Allerdings sind die Spiralen linksgŠngig, so wie die Konterspiralen der Abbildung 19b.
Abb. 20: Schmiedeeiserne Verzierung
Die Abbildung 21 zeigt die Situation der Abbildung 19 von oben. Die Spiralen erscheinen als Kreise.
Abb. 21: Sicht von oben
7 Rhombenfiguren
Die Abbildung 22 zeigt eine Diskretisierung mit Rhomben.
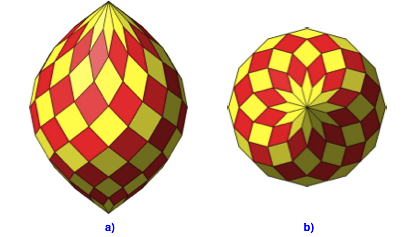
Abb. 22: Rhomben