Hans Walser, [20191109]

Kreis

Anregung: Zvonimir Durcevic, Wien

1     Worum geht es?

Abstandseigenschaften des Kreises

2     Erinnerung an die Schule

Der Kreis wird in der Schule gewšhnlich definiert als die Menge aller Punkte P, welche von einem gegebenen Punkt M konstanten Abstand haben:

 

                                                                                                                       (1)

 

 

 

 

Dabei sind M der Mittelpunkt und r der Radius des Kreises. Wir haben den Mittelpunkt als einzigen Bezugsprunkt.

Der Thaleskreis hingegen wird definiert als die Menge aller Punkte P, welche die Eigenschaft

 

                                                                                                 (2)

 

 

 

 

erfźllen. Wir haben die beiden Bezugspunkte A und B.

Wir werden sehen, dass (1) und (2) SonderfŠlle eines allgemeineren Sachverhaltes sind.

3     Allgemein

Wir arbeiten mit n Punkten  als Bezugspunkten. Weiter seien n Gewichte  gegeben. Wir zeigen, dass die Menge aller Punkte P mit der Eigenschaft

 

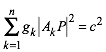                                                                                                       (3)

 

 

 

 

einen Kreis definieren.

In einem kartesischen Koordinatensystem verwenden wir die Schreibweisen  und . Fźr (3) erhalten wir:

 

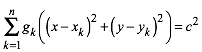                                                                       (4)

 

 

 

 

Weiter verwenden wir die Abkźrzung:

 

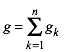                                                                                                                     (5)

 

 

 

 

Mit Hilfe von (5) lŠsst sich (4) umformen zu:

 

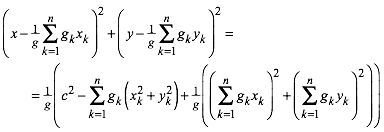         (6)

 

 

 

 

 

 

 

 

Dies ist die Gleichung eines Kreises. Dies war zu zeigen.

Der Kreis hat den Mittelpunkt M:

 

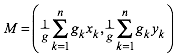                                                                               (7)

 

 

 

 

Der Mittelpunkt M ist also das gewichtete arithmetische Mittel der n Bezugspunkte.

Fźr den Radius r ergibt sich:

 

 

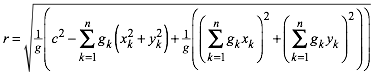             (8)

 

 

 

 

 

Wegen dem Minuszeichen im Radikanden von (8) ist der Radius nicht immer reell. Die Formel (8) erinnert an die Berechnung der empirischen Varianz.

4     Beispiele

4.1    Ein Bezugspunkt

Fźr  erhalten wir den Kreis der Abbildung 1. Das war zu erwarten.

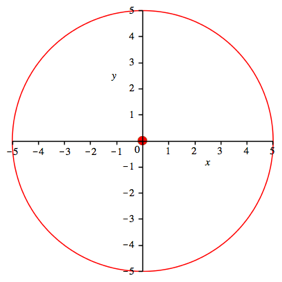
Abb. 1: Kreis mit Radius 5

Fźr  (Verdoppelung des Gewichtes) erhalten wir den Kreis der Abbildung 2. Der Radius reduziert sich auf .

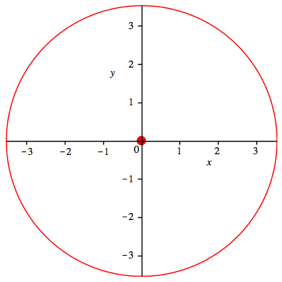
Abb. 2: Reduzierter Radius

Fźr  (Halbierung des Gewichtes) erhalten wir den Kreis der Abbildung 3. Der Radius vergrš§ert sich auf .

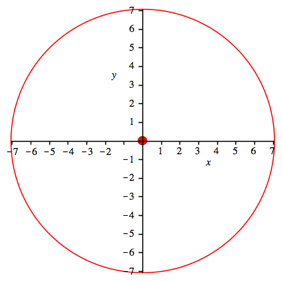
Abb. 3: Vergrš§erter Radius

4.2    Zwei Bezugspunkte

Die Bezugspunkte sind im folgenden grźn eigezeichnet, der Kreismittelpunkt rot.

In der Abbildung 4 ist c = 2. Wir erhalten den gewšhnlichen Thaleskreis.

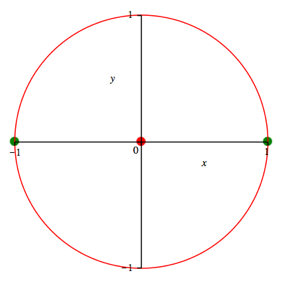
Abb. 4: Thaleskreis

4.2.1   Variation von c

Fźr c = 3, aber gleichbleibenden Bezugspunkten, erhalten wir einen vergrš§erten Radius (Abb. 5). Der Radius ist .

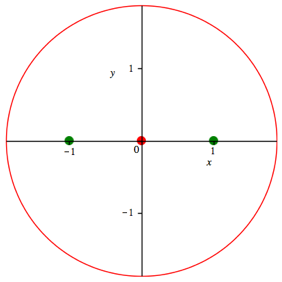
Abb. 5: Vergrš§erter Radius

Fźr c = 1.5 ergibt sich ein verkleinerter Radius (Abb. 6). Der Radius ist .

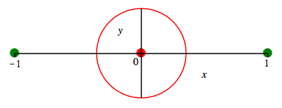
Abb. 6: Verkleinerter Radius

Fźr  ergibt sich der Radius null. Fźr  ergibt sich ein rein imaginŠrer Radius.

4.2.2   Variation der Gewichte

Wir setzen c = 2, aber beide Gewichte auf . Damit erhalten wir den Radius  (Abb. 7).

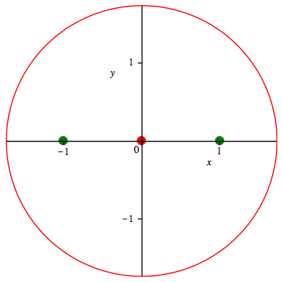
Abb. 7: Halbierung der Gewichte

Wenn wir nur ein Gewicht halbieren, ergibt sich eine asymmetrische Figur (Abb. 8). Das Gewicht des linken Punktes ist 1, das des rechten Punktes  und . Es ist  und .

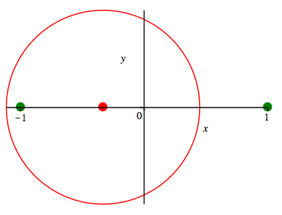
Abb. 8: Asymmetrisch

4.3    Drei Bezugspunkte

Im Beispiel der Abbildung 9 bilden die Bezugspunkte ein gleichseitiges Dreieck. Alle Gewichte sind 1 und . Wir erhalten den Umkreis.

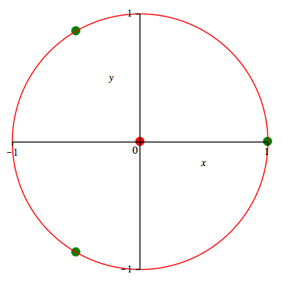
Abb. 9: Umkreis

Die Abbildung 10 zeigt ein unregelmŠ§iges Beispiel.

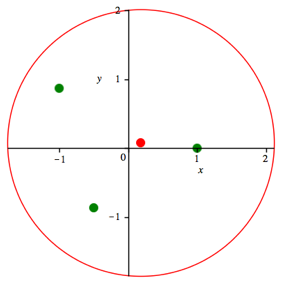
Abb. 10: UnregelmŠ§iges Beispiel

4.4    Vier Bezugspunkte

Im Beispiel der Abbildung 11 sind alle Gewichte 1 und . Wir erhalten den Umkreis.

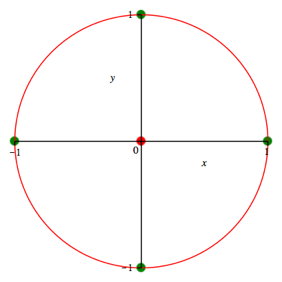
Abb. 11: Umkreis

Die Abbildung 12 zeigt ein unregelmŠ§iges Beispiel.

 

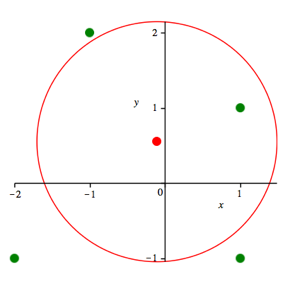
Abb. 12: UnregelmŠ§iges Beispiel

4.5    Fźnf Bezugspunkte

Alle Gewichte 1. .

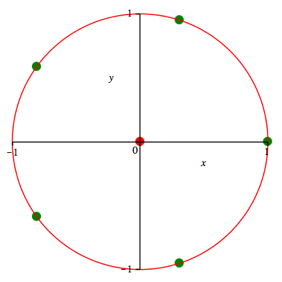
Abb. 13: RegelmŠ§iger Fall

Ich vermute, dass es allgemein fźr  den Umkreis gibt.

 

5     Kugel

Die †berlegungen lassen sich sinngemŠ§ auf die Kugel źbertragen.