Hans Walser, [20160516]

Kreisdarstellung

1 Zwei Glücksräder

In einem Schulbuch findet man die Abbildung 1a (Nachzeichnung des Autors) und etwas weiter hinten die Abbildung 1b (ebenfalls Nachzeichnung des Autors).

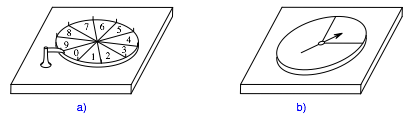
Abb. 1: Glücksräder

Beide Abbildungen sollen Glücksräder darstellen. Die Gegenüberstellung der beiden Abbildungen zeigt aber, dass (mindestens) eine Figur falsch sein muss. Welche?

Gefühlsmäßig halten wir die Figur der Abbildung 1a für falsch. Der Kreis scheint Schlagseite zu haben.

2 Kreis im Schrägbild

Die Bodenplatten der beiden Glücksräder sind im Schrägbild gezeichnet. Wir nehmen an, dass die Bodenplatten quadratisch sind.

Der Inkreis eines Quadrates berührt die Quadratseiten in den Seitenmittelpunkten (Abb. 2a). Das Schrägbild ist teilverhältnistreu ist, das heißt Mitte bleibt Mitte. Daher muss der Inkreis im Schrägbild aussehen gemäß Abbildung 2b.

Abb. 2: Inkreis im Quadrat

Nun ist offensichtlich, dass die Abbildung 1b die richtige ist.

3 Diskussion des Fehlers

Das Kreisbild der Abbildung 1a hat eine horizontale Symmetrieachse. Dies ist in vielen Abbildungsarten so (Foto, Normalprojektion). Daher meinen wir zunächst, das müsse in jeder Abbildung so sein. Im korrekten Schrägbild sind aber die Symmetrieachsen der Kreisbilder schräg.

Die Abbildung 3 zeigt einen Inkreis in Normalprojektion (Normalaxonometrie). Das Bild des Inkreises hat nun eine bezüglich des Zeichenblattes horizontale Symmetrieachse.

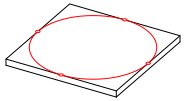
Abb. 3: Normalprojektion

Natürlich hätte man die Glücksräder auch auf der Basis der Abbildung 3 zeichnen können. Das würde natürlicher wirken als das Schrägbild.

4 Didaktische Bemerkung

Das Schrägbild ist in der Schule sehr beliebt, da es sich leicht auf Karopapier zeichnen lässt. Das geht so lange gut, als man es mit Polyedern zu tun hat. Sobald das „Runde“ ins Spiel kommt (Kreis, Kugel, Zylinder, Kreiskegel) wird das Schrägbild sehr kompliziert und unanschaulich. Man ist daher versucht, falsche Zeichenelemente hinein zu mogeln, wie das in der Abbildung 1a geschehen ist.