Hans Walser, [20170218]
Kreise im Goldenen Schnitt
1 Ausgangsfiguren
Es sei (Goldener Schnitt, Walser 2013):
Zum
Einheitskreis werden vier Kreise mit den Radien 
gezeichnet
(Abb. 1). Die Radien bilden also eine geometrische Folge mit dem Goldenen
Schnitt als Folgenquotient.
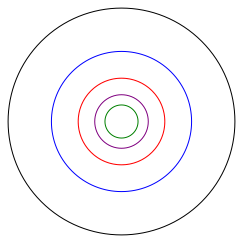
Abb. 1: Ausgangsfiguren
2 Berźhrende Anordnungen
Wir kšnnen diese Kreise sukzessive berźhrend anordnen.
Die zwei grš§ten Kreise (Major und Minor) passen in den Einheitskreis (Abb. 2).
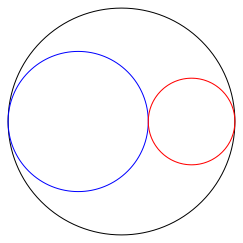
Abb. 2: Major und Minor
Durch Iteration kšnnen wir einen weiteren Kreis (lila) der Serie einpassen (Abb. 3).
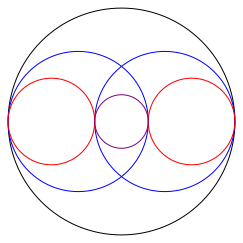
Abb. 3: Dritter Kreis
Die Figuren der Abbildungen 2 und 3 ergeben sich unmittelbar aus den Eigenschaften des Goldenen Schnittes.
Und nun kommt eine erste †berraschung: den lila Kreis kšnnen wir auch oben und unten berźhrend einpassen (Abb. 4). Das ist nicht trivial. Ich habe es durch Nachrechnen verifiziert.
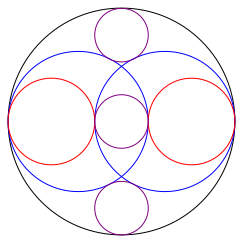
Abb. 4: Einpassen des kleinsten Kreises
Nun kšnnen wir aus Symmetriegrźnden weitere Kreise einfźgen (Abb. 5).
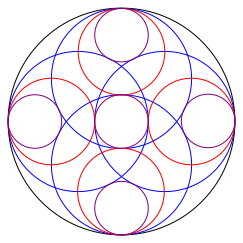
Abb. 5: Weitere Kreise
Und nun folgt die zweite †berraschung: wir kšnnen vier weitere lila Kreise einpassen (Abb. 6).
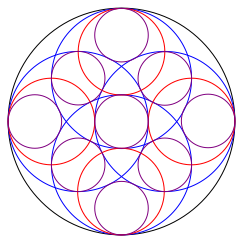
Abb. 6: Vier weitere lila Kreise
Auch dies ist nicht trivial und muss verifiziert werden. Die insgesamt neun lila Kreise liegen in einem quadratischen 3×3-Raster. Auch dies muss verifiziert werden.
Die vier neuen lila Kreise berźhren die blauen Kreise (Majore) in den Schnittpunkten der blauen Kreise mit den roten Kreisen (Minore). Die Schnittwinkel sind rechte Winkel.
In der Abbildung 7 sind die roten Kreise (Minore) weggelassen.
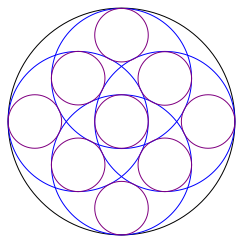
Abb. 7: Ohne Minore
Und jetzt kšnnen wir noch zwšlf grźne Kreise einpassen (Abb. 8). Fźr die vier grźnen Kreise zwischen den lila Kreisen folgt das aus den Eigenschaften des Goldenen Schnittes. Fźr die acht grźnen Kreise, welche auch den schwarzen Randkreis berźhren, ist das wiederum eine †berraschung und muss verifiziert werden. Die grźnen Kreise sind ebenfalls in einem Quadratraster angeordnet.
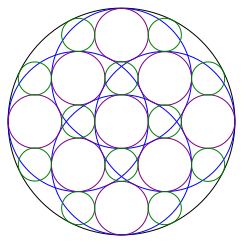
Abb. 8: Die ganz kleinen
In der Abbildung 9 sind die blauen Kreise (Majore) weggelassen.
Abb. 9: Kreispackung im Goldenen Schnitt
Wir źberlegen mit dynamischer Kopfgeometrie, dass diese Figuren nur mit Kreisen im RadienverhŠltnis des Goldenen Schnittes funktionieren.
Literatur
Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.