Hans Walser, [20140128]
Kreise in Karten
Anregung: D. H., L.
1 Worum geht es?
Wie werden Kreise auf der Kugel in verschiedenen Karten dargestellt?
2 Kreise auf der Kugel
Die Abbildung 1 zeigt die Kugel mit dem źblichen Netz von Meridianen und Breitenkreisen in rot. Die Maschenweite des Netzes ist 15ˇ.

Abb. 1: Kugel mit Meridianen und Breitenkreisen
In der Abbildung 2 ist
zusŠtzlich ein weiteres Netz in blau
eingezeichnet. Es besteht aus Kro§kreisen mit zwei gemeinsamen Punkten (blaue
Pole) und den dazu orthogonalen Kreisen. Der nšrliche blaue Pol hat die
geografische Breite 45ˇN. Wir haben also ein schiefachsiges Netz.

Abb. 2: Roter Pol auf 45ˇN
In der Abbildung 3 sind die blauen Pole auf dem €quator (querachsige Disposition).

Abb. 3: Querachsig
Die Frage ist nun, wie diese blauen Netze in verschiedenen Karten aussehen.
3 Plattkarte
Die Abbildung 4 zeigt die Plattkarte.
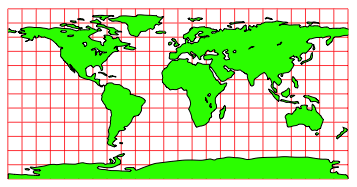
Abb. 4: Plattkarte
In der Abbildung 5 ist zusŠtzlich das schiefachsige blaue Netz eingetragen.
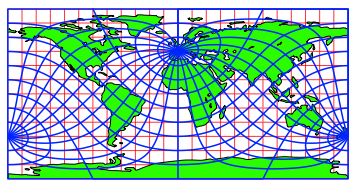
Abb. 5: Schiefachsiges Netz
Das blaue Netz gibt Anlass zu einem zweidimensionalen Ornament (Abb. 6).
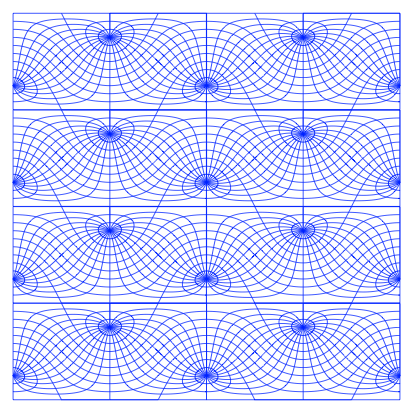
Abb. 6: Ornament
In der Abbildung 7 ist das querachsige blaue Netz eingetragen.
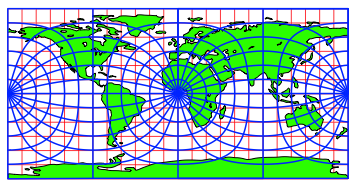
Abb. 7: Querachsiges Netz
4 FlŠchentreue Karte von Archimedes-Lambert
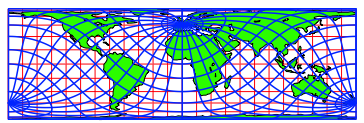
Abb. 8: Schiefachsiges Netz
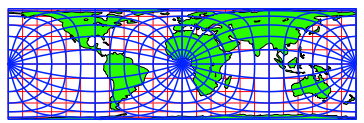
Abb. 9: Querachsiges Netz
5 Winkeltreue Karte von Mercator (Seekarte)
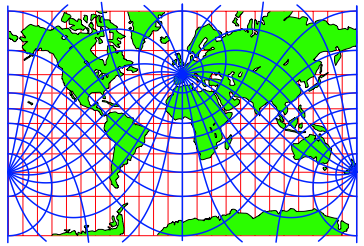
Abb. 10: Schiefachsiges Netz
Die Kurvenscharen schneiden sich źberall orthogonal.
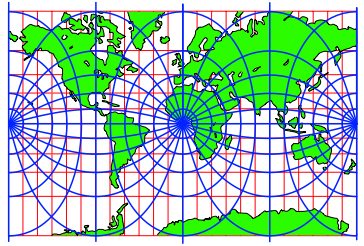
Abb. 11: Querachsiges Netz
Die Bilder der Kleinkreise sind keine Ellipsen. Zum Vergleich ist in Abbildung 12 eine Ellipse eingetragen. Sie weicht leicht vom Bild des Kleinkreises ab.
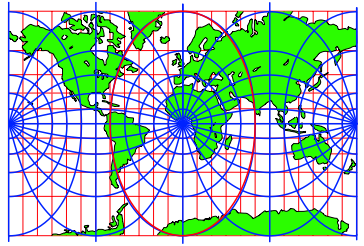
Abb.12: Ellipse?
6 FlŠchentreue Karte von Mercator-Sanson
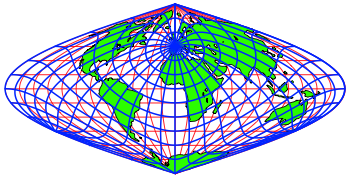
Abb. 13: Schiefachsiges Netz
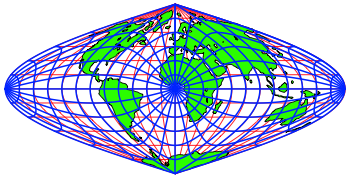
Abb. 14: Querachsiges Netz