Hans Walser, [20180718]
Kreise und Ellipsen
1 Worum es geht
Wir setzen n Kreise nebeneinander und zeichnen die Ellipse, welche die beiden u§ersten Kreise ganz au§en optimal berhrt.
Die Abbildung 1 zeigt die Situation fr n = 5.
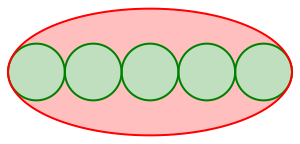
Abb. 1: Fnf Kreise und eine Ellipse
Die ãoptimale BerhrungÒ meint, dass die beiden u§ersten Kreise Scheitelkrmmungskreise der Ellipse sind.
Alles in allem eine Spielerei.
2 Berechnungen
Fr die Berechnungen setzen wir die Kreisradien auf 1. Die Ellipse habe wie blich die Halbachsen a und b. Der Krmmungskreisradius am spitzen Scheitel ist:
![]() (1)
(1)
Wegen der verlangten optimalen Berhrung ist:
![]() (2)
(2)
Weiter ist:
![]() (3)
(3)
Aus (2) und (3) folgt:
![]() (4)
(4)
3 Beispiele
3.1 Ein Kreis
Der Kreis und die Ellipse fallen zusammen.
3.2 Zwei Kreise
Die Figur lsst sich in ein Rechteck im DIN-Format einpassen (Abb. 2b) [1]. ber das DIN-Format siehe Walser (2013b).
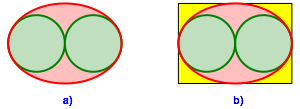
Abb. 2: DIN-Format
Die Ellipse berhrt in den Scheiteln optimal, ist aber nicht optimal im Sinne des kleinsten Flcheninhaltes [2] .
3.3 Drei Kreise
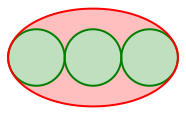
Abb. 3: Drei Kreise
Die Figur lsst sich mit gleichseitigen Dreiecken in Beziehung bringen (Abb. 4).
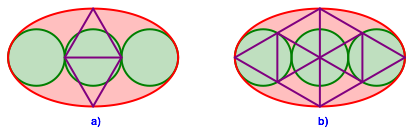
Abb. 4: Mit gleichseitigen Dreiecken
Die Abbildung 5 zeigt eine berlagerung von drei Figuren der Abbildung 3, vgl. [3].
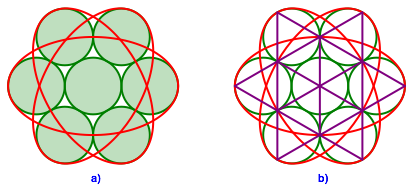
Abb. 5: Sieben Kreise
3.4 Vier Kreise
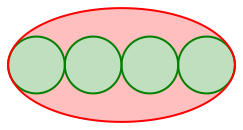
Abb. 6: Vier Kreise

Abb. 7: Vier mal vier Kreise

Abb. 8: Tetraktys
Die Tetraktys-Figur (Abb. 8) enthlt viele falsche Freunde. Scheinbare Schnittpunkte von drei Ellipsen sind keine, scheinbare Berhrungspunkte von zwei Ellipsen sind keine, der Umriss ist keine Reuleaux-Figur. Die Figur ist nicht konvex.
3.5 Fnf Kreise
Die Abbildung 1 zeigt die Situation mit fnf Kreisen.
Das umschlie§ende Rechteck lsst sich in insgesamt zehn Goldene Rechtecke (gelb, zyan, orange) unterteilen. ber Goldene Rechtecke siehe Walser (2013a, S. 53).
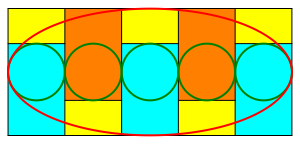
Abb. 9: Unterteilung in Goldene Rechtecke
3.6 Synopsis
Die Abbildung 10 zeigt eine Synopsis der bisherigen Figuren.
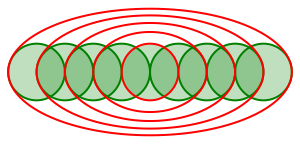
Abb. 10: Synopsis
Die berlappenden Kreise bilden Zweiecke. Wir passen in diese Zweiecke Ellipsen ein, welche in den Punkten links und rechts optimal berhren (Abb. 11). Diese Ellipsen sind hnlich zur Ellipse der Abbildung 2.
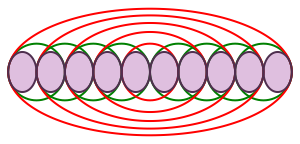
Abb. 11: Stehende Ellipsen
3.7 Synopsis mit Parabel
Die Abbildung 12 zeigt eine andere Anordnung der Ellipsen. Die stumpfen Scheitel der Ellipsen liegen auf einer liegenden Parabel.
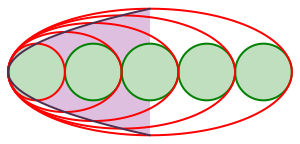
Abb. 12: Parabel
3.8 Neun mal neun Kreise
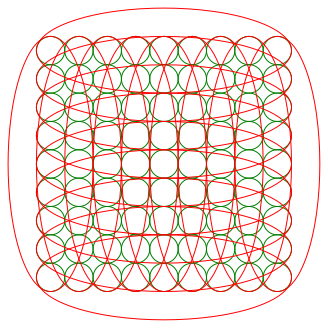
Abb. 13: Neun mal neun Kreise
Websites
[1] Hans Walser: Ellipsen im DIN-Format (abgerufen 18.07.2018):
www.walser-h-m.ch/hans/Miniaturen/E/Ellipsen_DIN/Ellipsen_DIN.htm
[2] Hans Walser: Minimalellipse (Abgerufen 18.07.2018):
www.walser-h-m.ch/hans/Miniaturen/M/Minimalellipse/Minimalellipse.htm
[3] Hans Walser: Orthogonale Gro§kreise in isometrischer Darstellung (abgerufen 19.07.2018):
www.walser-h-m.ch/hans/Miniaturen/O/Orth_Grosskreise/Orth_Grosskreise.htm
Literatur
Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.
Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.