Hans Walser, [20091118a]
Kreisfcher
1
Kreisfcher

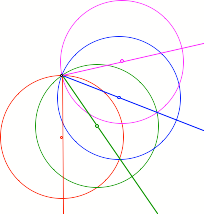
Kreisfcher
Wir arbeiten in einem
Fcher aus kongruenten Kreisen mit konstanten Fcherwinkel ![]() .
.
2 Schnittpunkte
2.1
Vier Kreise
Bei einem Fcher von
vier Kreisen sehen wir, dass einige Schnittpunkte von Fcherkreisen kollinear
sind.
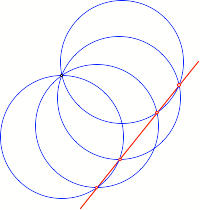
Kollineare Punkte
2.2
Mehrere Kreise
Wenn wir den Fcher
vergr§ern, erhalten wir zustzliche Quadrupel kollinearer Punkte.
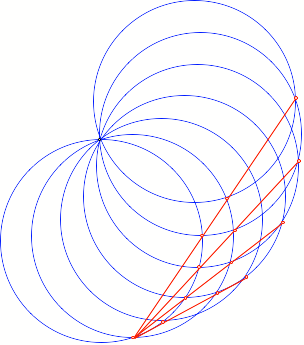
Fcher mit mehreren
Kreisen
3
Beweis
Wir beweisen den Fall
mit einem Fcher mit vier Kreisen. Fr gr§ere Fcher luft der Beweis analog.
Allerdings fhren wir
fr den Beweis noch einen fnften Kreis an. Bezeichnungen gem§ Figur.
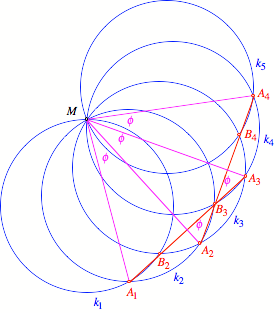
Beweisfigur
Es sei ![]() der Schnittpunkt
der beiden Strecken
der Schnittpunkt
der beiden Strecken ![]() und
und ![]() . Zu zeigen ist, dass
. Zu zeigen ist, dass ![]() auch der
Schnittpunkt der beiden Kreise
auch der
Schnittpunkt der beiden Kreise ![]() und
und ![]() ist.
ist.
Wegen der Fcherung ist
die Strecke ![]() die um den
Fcherwinkel
die um den
Fcherwinkel ![]() gedrehte Strecke
gedrehte Strecke
![]() . Wir haben also bei
. Wir haben also bei ![]() den
Schnittwinkel
den
Schnittwinkel ![]() der beiden Strecken.
der beiden Strecken.
Nun ist aber, ebenfalls
auf Grund der Fcherkonstruktion, der Kreis ![]() der Ortsbogen
(Fasskreis) ber der Strecke
der Ortsbogen
(Fasskreis) ber der Strecke ![]() fr den
Peripheriewinkel
fr den
Peripheriewinkel ![]() . Daher liegt
. Daher liegt ![]() auf
dem Kreis
auf
dem Kreis ![]() . Analog ist der Kreis
. Analog ist der Kreis ![]() der Ortsbogen
(Fasskreis) ber der Strecke
der Ortsbogen
(Fasskreis) ber der Strecke ![]() fr denselben
Peripheriewinkel
fr denselben
Peripheriewinkel ![]() . Daher liegt
. Daher liegt ![]() auch auf dem
Kreis
auch auf dem
Kreis ![]() . Somit ist
. Somit ist ![]() der Schnittpunkt
der beiden Kreise.
der Schnittpunkt
der beiden Kreise.
Analog kann gezeigt
werden, dass die Strecke ![]() auch durch den
Schnittpunkt
auch durch den
Schnittpunkt ![]() der beiden
Kreise
der beiden
Kreise ![]() und
und ![]() verluft.
verluft.
4
Regelm§ige Vielecke. Bildergalerie
Wenn wir in einem
regelm§igen n-Eck ![]() mit dem
Mittelpunkt M die Umkreise
mit dem
Mittelpunkt M die Umkreise ![]() der
Sektordreiecke
der
Sektordreiecke ![]() zeichnen, ergibt
sich ein Fcher mit n Kreisen und
dem Fcherwinkel
zeichnen, ergibt
sich ein Fcher mit n Kreisen und
dem Fcherwinkel ![]() . Die Diagonalen verlaufen immer durch (mindestens) 4 Schnittpunkte
dieser Fcherkreise (bei geradem n
muss der Mittelpunkt doppelt gezhlt werden).
. Die Diagonalen verlaufen immer durch (mindestens) 4 Schnittpunkte
dieser Fcherkreise (bei geradem n
muss der Mittelpunkt doppelt gezhlt werden).
4.1
Quadrat
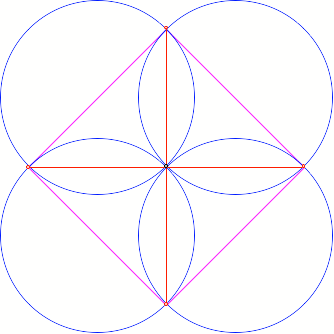
Kreisfcher im Quadrat
4.2
Pentagon
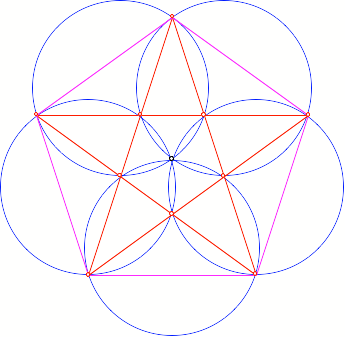
Kreisfcher im Pentagon
4.3
Hexagon
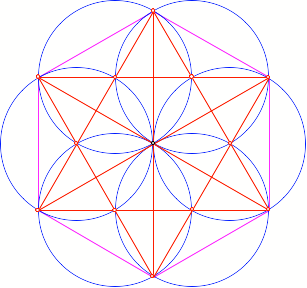
Kreisfcher im Hexagon
4.4
Regelm§iges Siebeneck
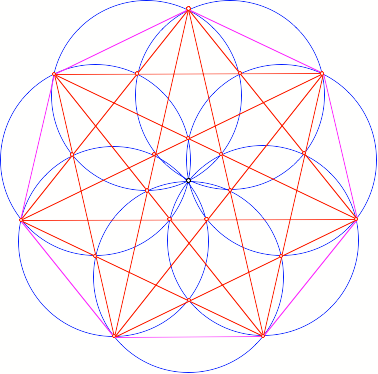
Kreisfcher im
regelm§igen Siebeneck
4.5
Regelm§iges Achteck
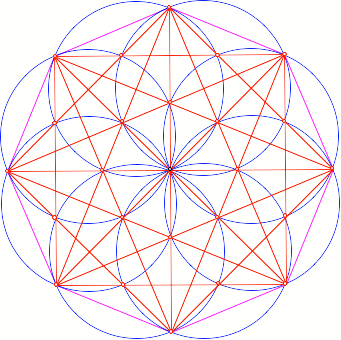
Kreisfcher im
regelm§igen Achteck
4.6
Regelm§iges Neuneck
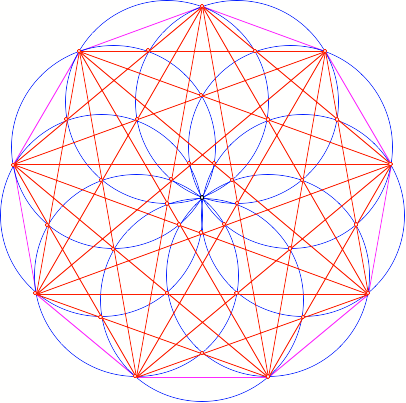
Kreisfcher im
regelm§igen Neuneck