Hans Walser, [20071228d], [20130922]
Die KreisflŠche
1 Worum geht es?
In den folgenden
†berlegungen gehen wir davon aus, dass wir die Formel 
fŸr den
Kreisumfang kennen, nicht aber die Formel fŸr den FlŠcheninhalt des Kreises.
Hingegen ist aus
€hnlichkeitsŸberlegungen klar, dass diese die Form 
mit vorlŠufig
unbekanntem Faktor p haben muss.
Es werden drei Beispiele vorgestellt, wie der Faktor p bestimmt werden kann.
2 Aufschneiden von Kreisringen
Wir denken uns einen Kreis, der aus vielen konzentrischen Ringen zusammengesetzt ist. Man kann sich auch den Querschnitt einer Papierrolle denken.
Der Kreis
Nun schneiden wir den Kreis von oben her bis in die Mitte ein und lassen die einzelnen BlŠtter links und rechts auf den Tisch herunterfallen. Die Figurensequenz zeigt das in Zeitlupe.
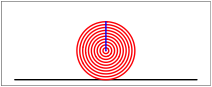
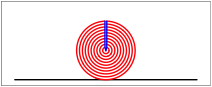
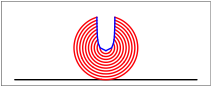
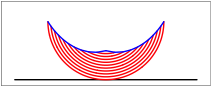
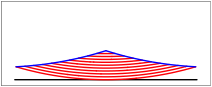
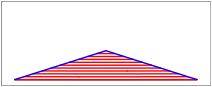
Die BlŠtter fallen, fallen wie von weit. (Rilke)
Wir haben schlie§lich
ein Dreieck; seine Hšhe ist der Kreisradius r,
seine Grundseite der Umfang 
des
ursprŸnglichen Kreises. FŸr den FlŠcheninhalt erhalten wir also:
Das ist aber auch der FlŠcheninhalt des Kreises.
Wir kšnnen die BlŠtter auch noch weiter herunterfallen lassen.
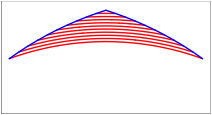
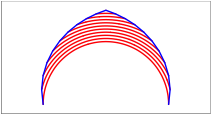
†berdreht
Am Schluss ist die rote FlŠche gleich gro§ wie die wei§e KreisflŠche.
RotkŠppchen
3 Klopapier
Da ich nach P... verreisen wollte, riet man mir, Toilettenpapier mitzunehmen. So packte ich eine Rolle in den Rucksack. Als ich sie vor Ort dringend brauchte und aus dem Rucksack holte, war sie zusammengedrŸckt (Abbildung rechts).
Klorolle, neu und zusammengedrŸckt
Nun kann folgende †berlegung angestellt werden.
Die Formel fŸr den
Kreisumfang kennen wir: 
Die Formel fŸr den
FlŠcheninhalt sieht so aus: 
, mit einem noch unbekannten Faktor p.
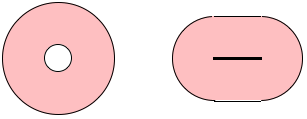
FŸr die Klorolle haben
wir einen Au§enradius 
und einen
Innenradius 
und damit eine
QuerschnittsflŠche:
Der Querschnitt der
zusammengedrŸckten Rolle setzt sich aus zwei Halbkreisen mit dem Radius 
und einem
Rechteck zusammen. Dieses Rechteck hat die Hšhe 
und die LŠnge 
; das ist der halbe Umfang des Innenkreises. FŸr die QuerschnittsflŠche
der zusammengedrŸckten Rolle erhalten wir somit:
Die beiden QuerschnittsflŠchen sind gleich, also:
Somit ist: 
4 Unterteilung der KreisflŠche
Wir unterteilen den Kreis in einen Teil.
Ein Teil
Meine Mutter gab bei allen passenden und unpassenden Gelegenheiten zum Besten, sie hŠtte einmal einen Kuchen gebacken und mir erlaubt, etwas davon abzuschneiden. Ich hŠtte dann von der Mitte her bis zum Rand geschnitten, und das StŸck gegessen.
Nun unterteilen wir in vier flŠchenmŠ§ig gleich gro§e Teile:
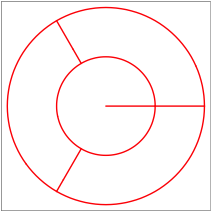
Vier gleich gro§e Teile
Dass die vier Teile flŠchenmŠ§ig gleich gro§ sind, kann so eingesehen werden: Der innere Kreis hat den halben Durchmesser wie der gro§e Kreis. Hat eine Figur die gleiche Form wie eine andere, ist aber lŠngenmŠ§ig nur halb so gro§, dann ist ihr FlŠcheninhalt nur ein Viertel des FlŠcheninhaltes der anderen Figur. Der Šu§ere Kreisring hat also noch den dreifachen FlŠcheninhalt des inneren StŸckes; durch Dritteln des Ringes ergeben sich zusammen mit dem inneren StŸck vier flŠchengleiche Teile.
In den folgenden beiden Figuren sehen wir eine Unterteilung in neun beziehungsweise 16 gleiche Teile. Diese sind in drei beziehungsweise vier Ringen angeordnet.
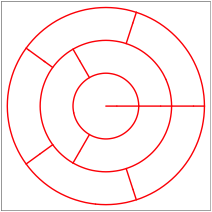
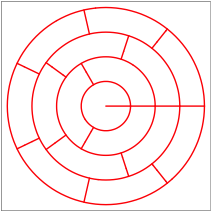
Neun beziehungsweise 16 gleich gro§e Teile
Die Ringe enthalten von
innen nach au§en 
Teile, und
insgesamt ergeben sich 
flŠchenmŠ§ig
gleich gro§e Teile.
In den beiden folgenden Figuren hat es 100 respektive 400 gleich gro§e Teile, angeordnet in 10 beziehungsweise 20 Ringen.
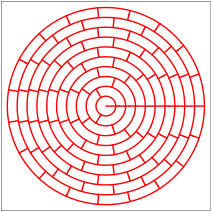
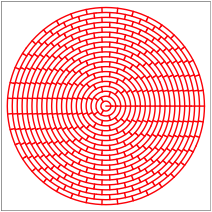
100 respektive 400 gleich gro§e Teile
Die 
Teile im
Šu§ersten Ring sind praktisch Rechtecke. Sie haben eine Breite von 
(r ist der Kreisradius). FŸr die LŠnge
machen wir eine Mittelrechnung: die Šu§ere LŠnge ist 
, die innere LŠnge ist 
. Damit ergibt sich eine mittlere LŠnge l:
FŸr ein einzelnes Rechteck erhalten wir somit den FlŠcheninhalt:
Der Kreis setzt sich
aus 
flŠchengleichen
Teilen zusammen, somit ist:
