Hans Walser, [20140507]
Kreisfunktionen
1 Worum geht es?
Es werden Integration und Ableitung der Kosinus- und der Sinusfunktion besprochen.
2 Definition der Kreisfunktionen
Wir verwenden die źblichen Definitionen im Einheitskreis (Abb. 1).
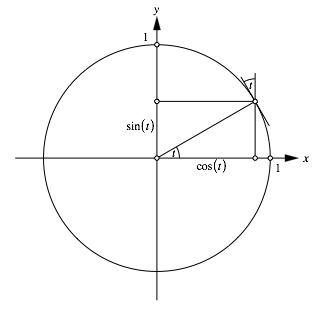
Abb. 1: Definition der Kreisfunktionen
Die Tangente schlie§t mit der Parallelen zur y-Achse ebenfalls den Winkel t ein.
3 Dispositionen global und lokal
Die Abbildung 2 zeigt die †bersicht.
Abb. 2: †bersicht
Die Abbildung 3 zeigt den relevanten lokalen Ausschnitt.
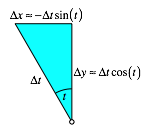
Abb. 3: Lokaler Ausschnitt
Die x-Werte nehmen ab, daher das Minuszeichen.
4 Grenzźbergang
Bei 
glŠtten
sich die ă
Ň-Zeichen.
4.1 Integrative †berlegung
Die integrative †berlegung ist global und summativ.
y-Richtung:
Die Sinusfunktion ist also eine Stammfunktion der Kosinusfunktion.
x-Richtung:
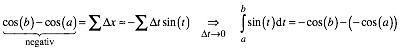
Die negative Kosinusfunktion ist also eine Stammfunktion der Sinusfunktion.
4.2 Differenzielle †berlegung
Die differenzielle †berlegung ist lokal.
y-Richtung:
Die Kosinusfunktion ist die Ableitung der Sinusfunktion.
x-Richtung:
Die negative Sinusfunktion ist die Ableitung der Kosinusfunktion.